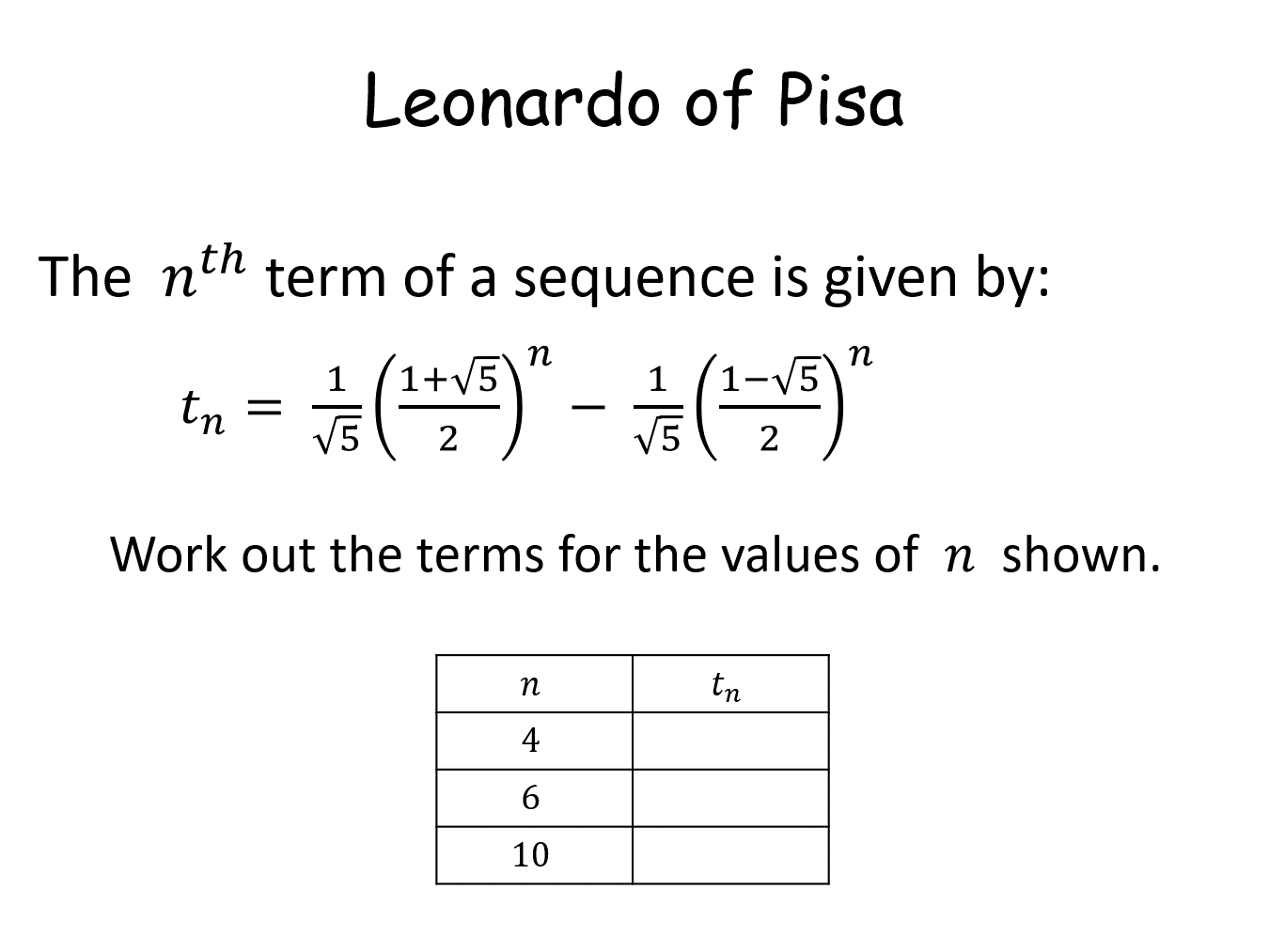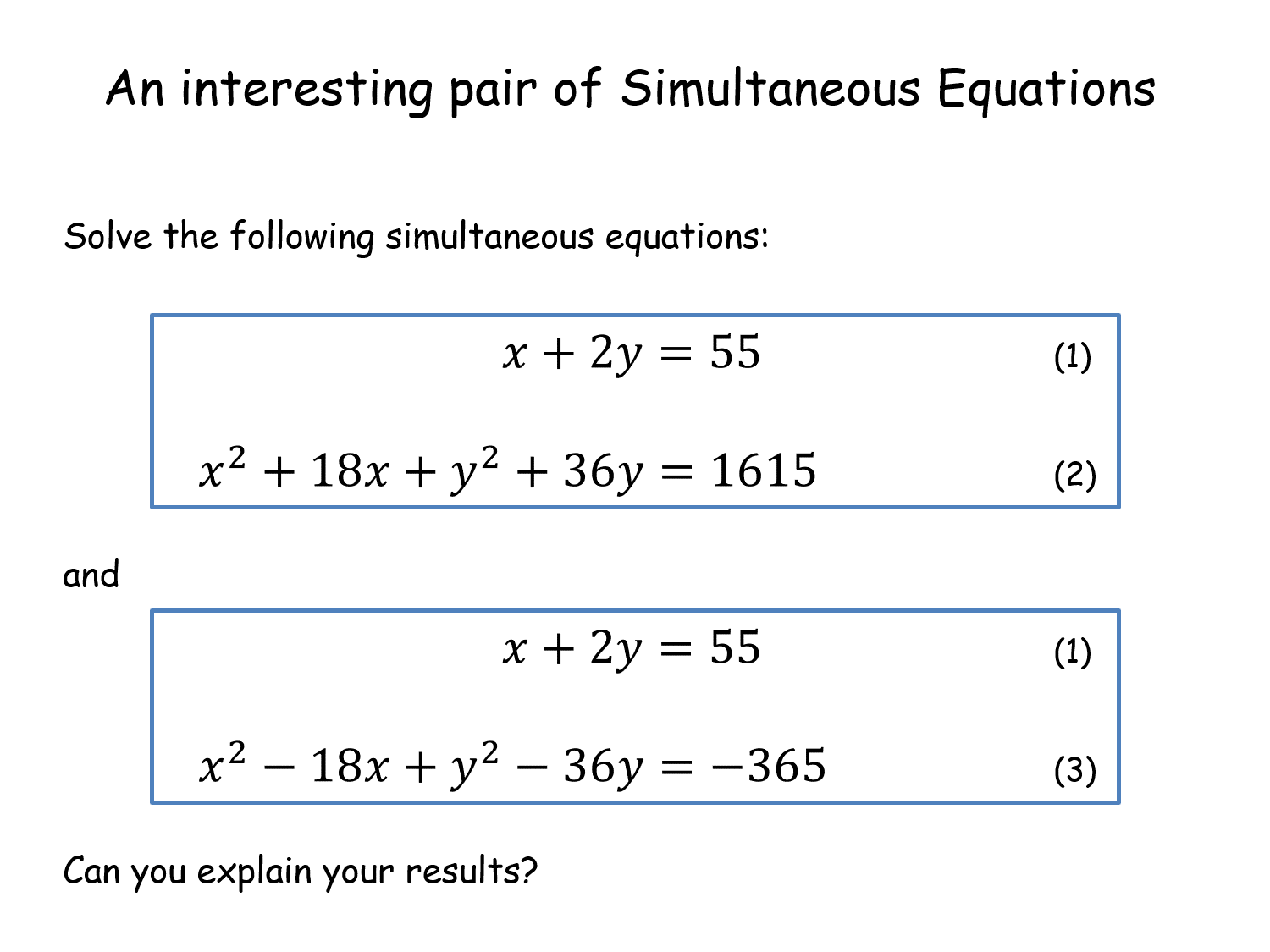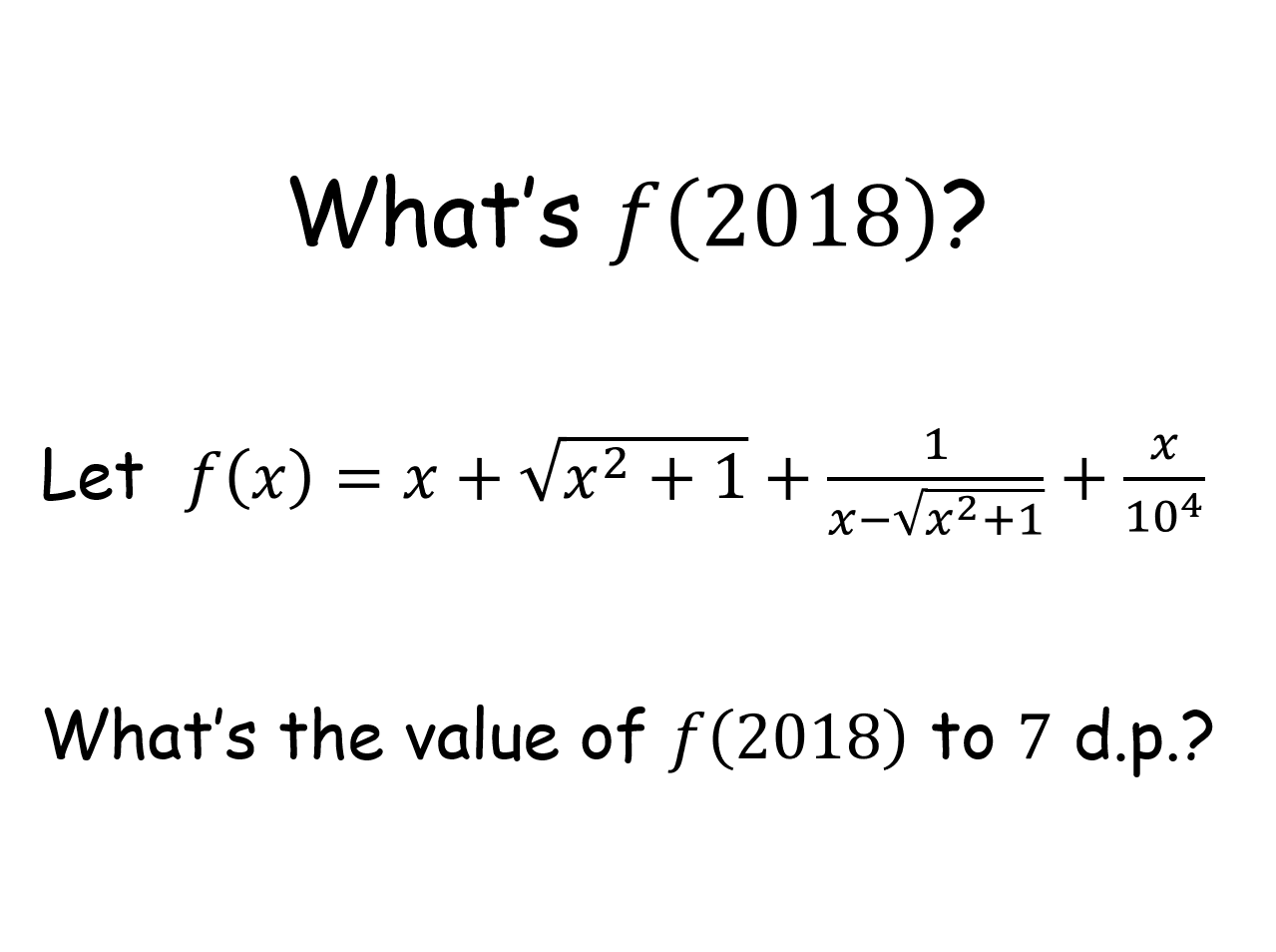| 1 |
Think of a Number |
A simple game that finishes on 1, whatever your starting number. Leads to creating expressions and proof. No worksheets are required.Think of a Number |
B_
Year 8
x_B_x |

| |
 (PowerPoint) (PowerPoint) |
|
|
|
| 2 |
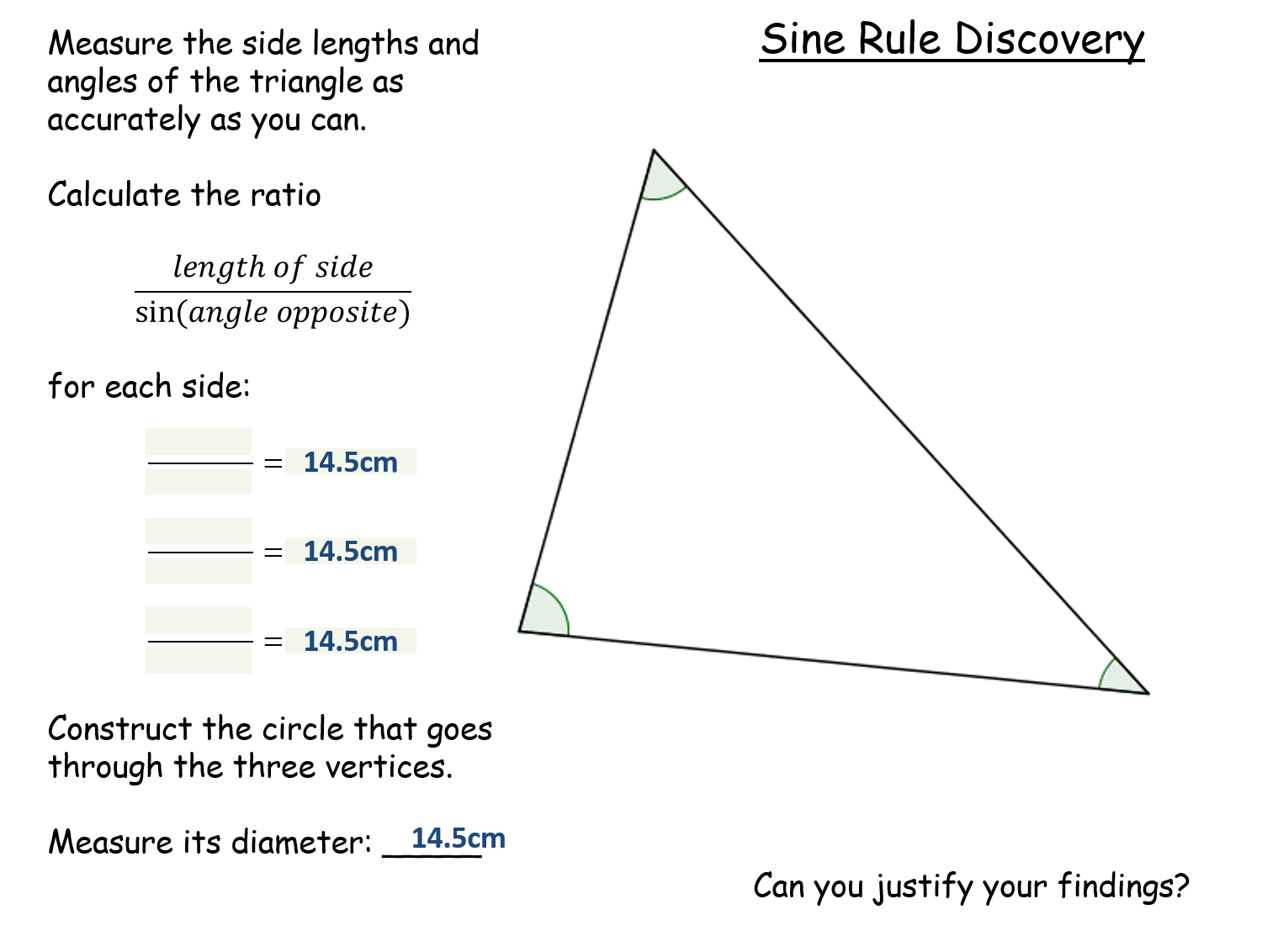
Sine Rule Discovery |
Measure the sides and angles and calculate the ratios. All ratios in the class are the same, yet all of the triangles are different.Sine Rule Discovery |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 3 |
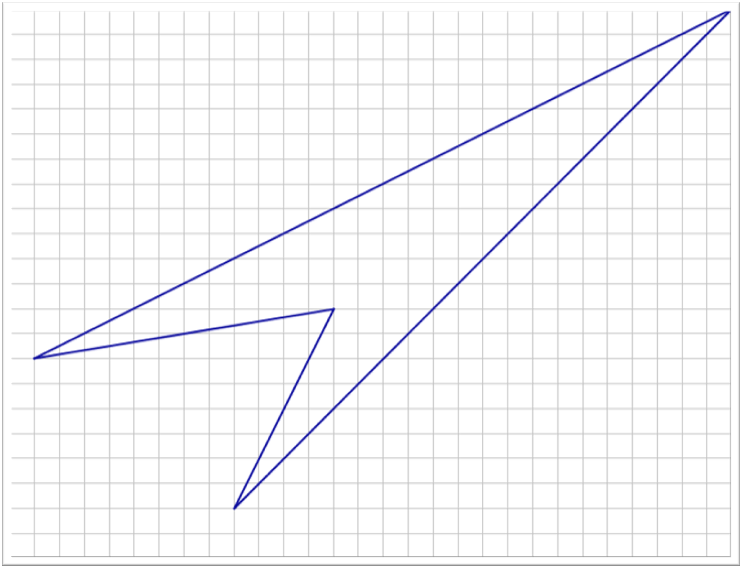
Parallelogram in Quadrilateral - Grid |
Bisect the sides of a quadrilateral to get a parallelogram (Varignon's Theorem). All quadrilaterals are different but all parallelograms are identical. The grid allows easy bisection.Parallelogram in Quadrilateral - Grid |
B_
Year 8
x_B_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 4 |
Parallelogram in Quadrilateral - Compass |
Bisect the sides of a quadrilateral to get a parallelogram. All quadrilaterals are different but all parallelograms are identical. A compass will be needed to bisect the sides.Parallelogram in Quadrilateral - Compass |
C_
Year 9
x_C_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 5 |
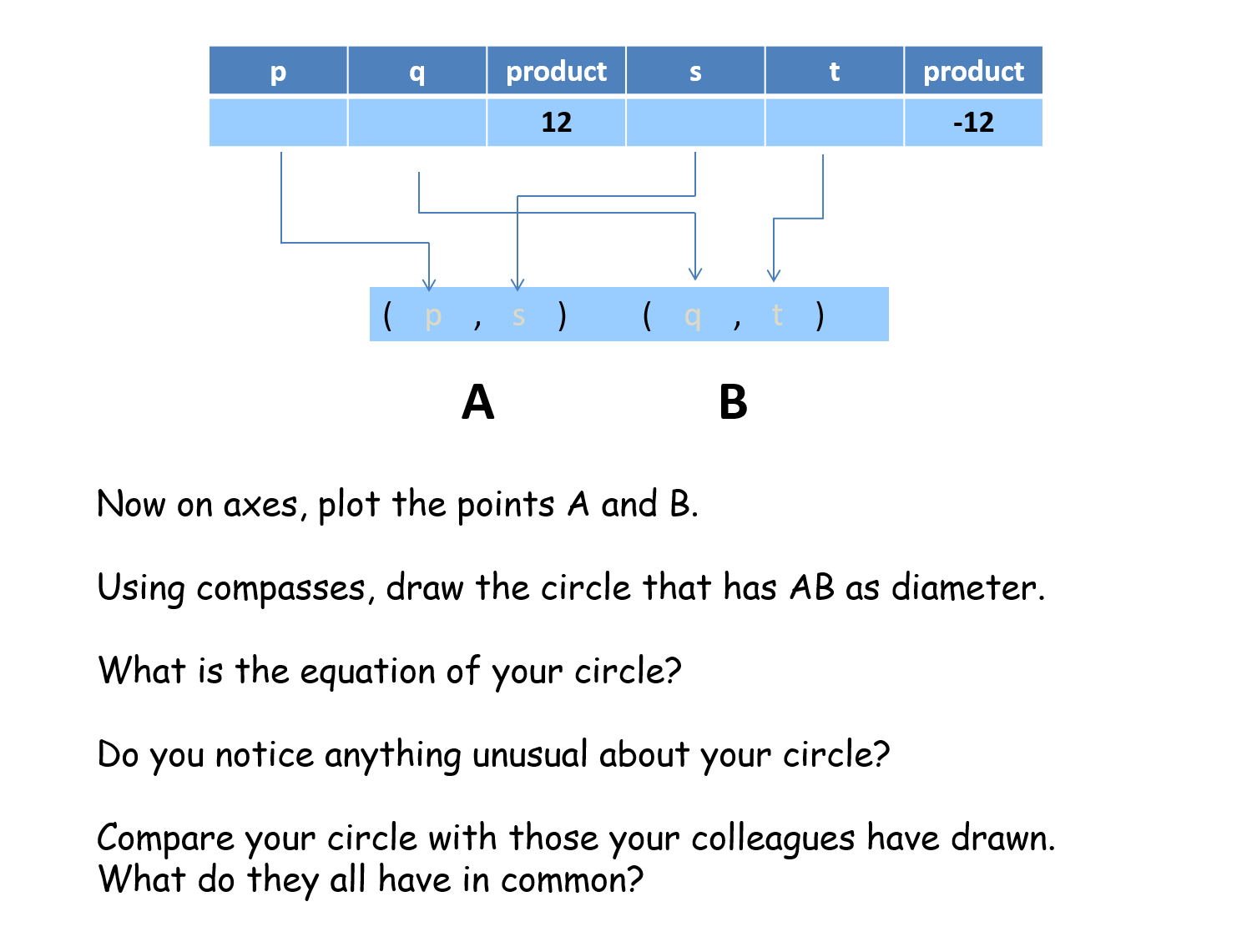
A Circle Property |
RISP 9. Pupils choose certain values and draw their own circle. All circles go through the origin.A Circle Property |
F
Year 1 - Pure
x_R_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 6 |
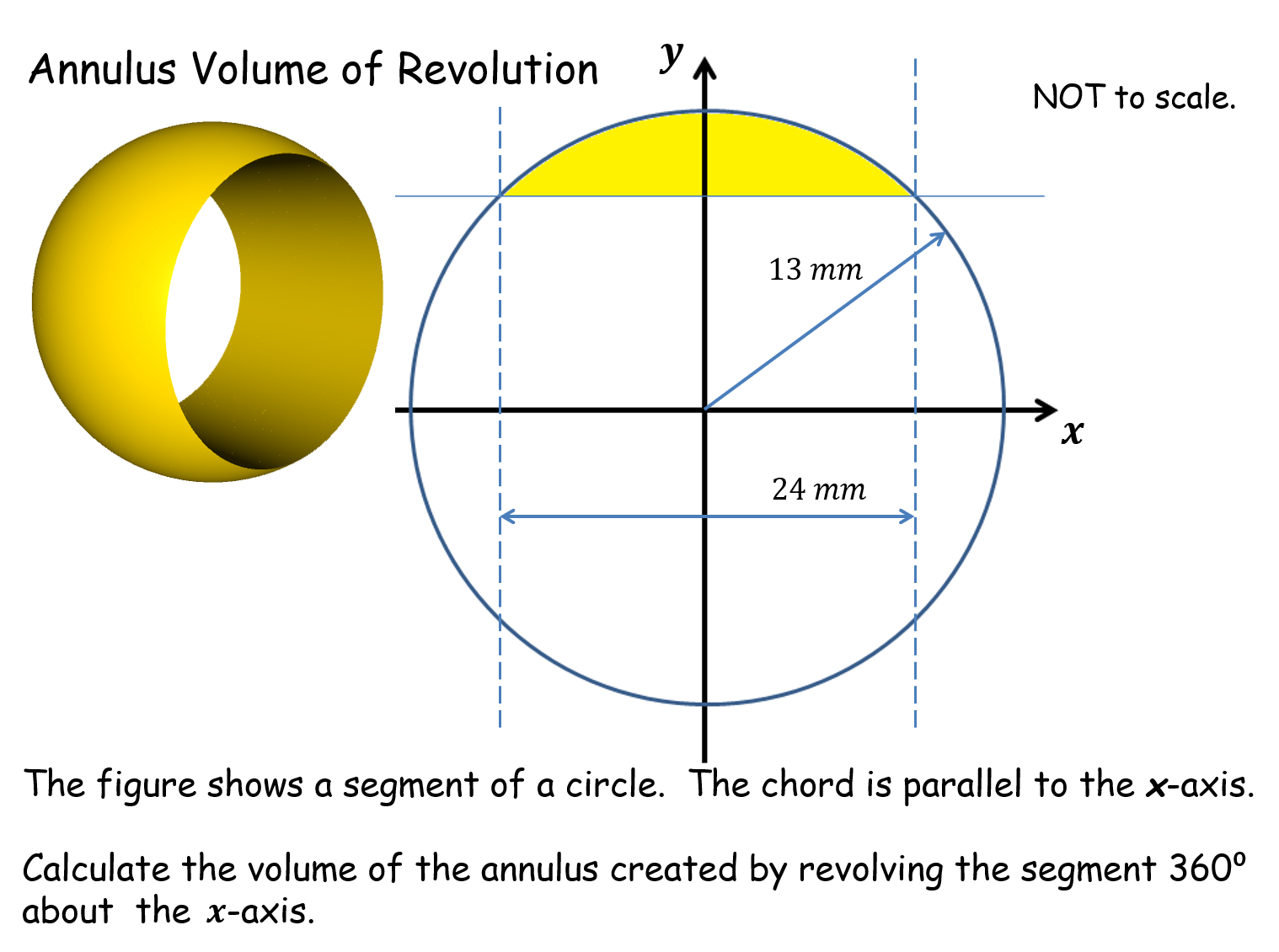
Annulus Volume of Revolution |
Pupils are given different segments of circles and asked to calculate their volumes of revolution. They all have the same volume.Annulus Volume of Revolution |
I
Year 1 - Further Pure
x_R_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Excel) (Excel) |
 (Autograph) (Autograph) |
|
| 7 |
Trapezium and Diagonals |
Pupils need to work out the area of two triangles given the area of two others which all fit in a trapezium. This problem acts as a good reminder that a triangle's area does not change as the apex moves parallel to the base. In solving this problem many pupils will use similarity, but there is a much more elegant solution.Trapezium and Diagonals |
C_
Year 9
x_C_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 8 |
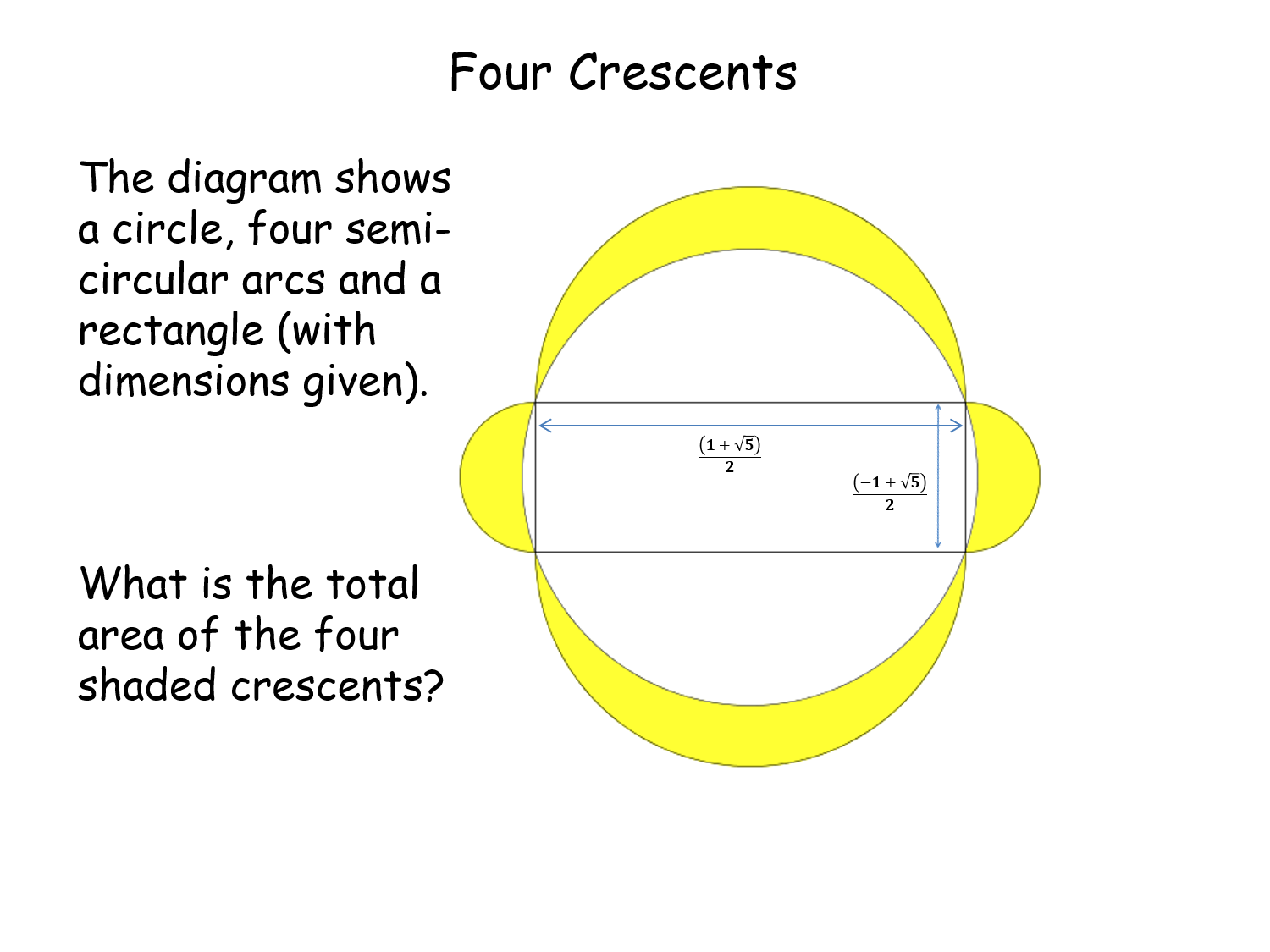
Four Crescents |
Four crescents are drawn around a rectangle. All rectangles are different and the area of the crescents is equal to that of the rectangle. Surd (area = 1) and non-surd (area = 900) versions available.Four Crescents |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Scratch) (Scratch) |
|
|
| 9 |
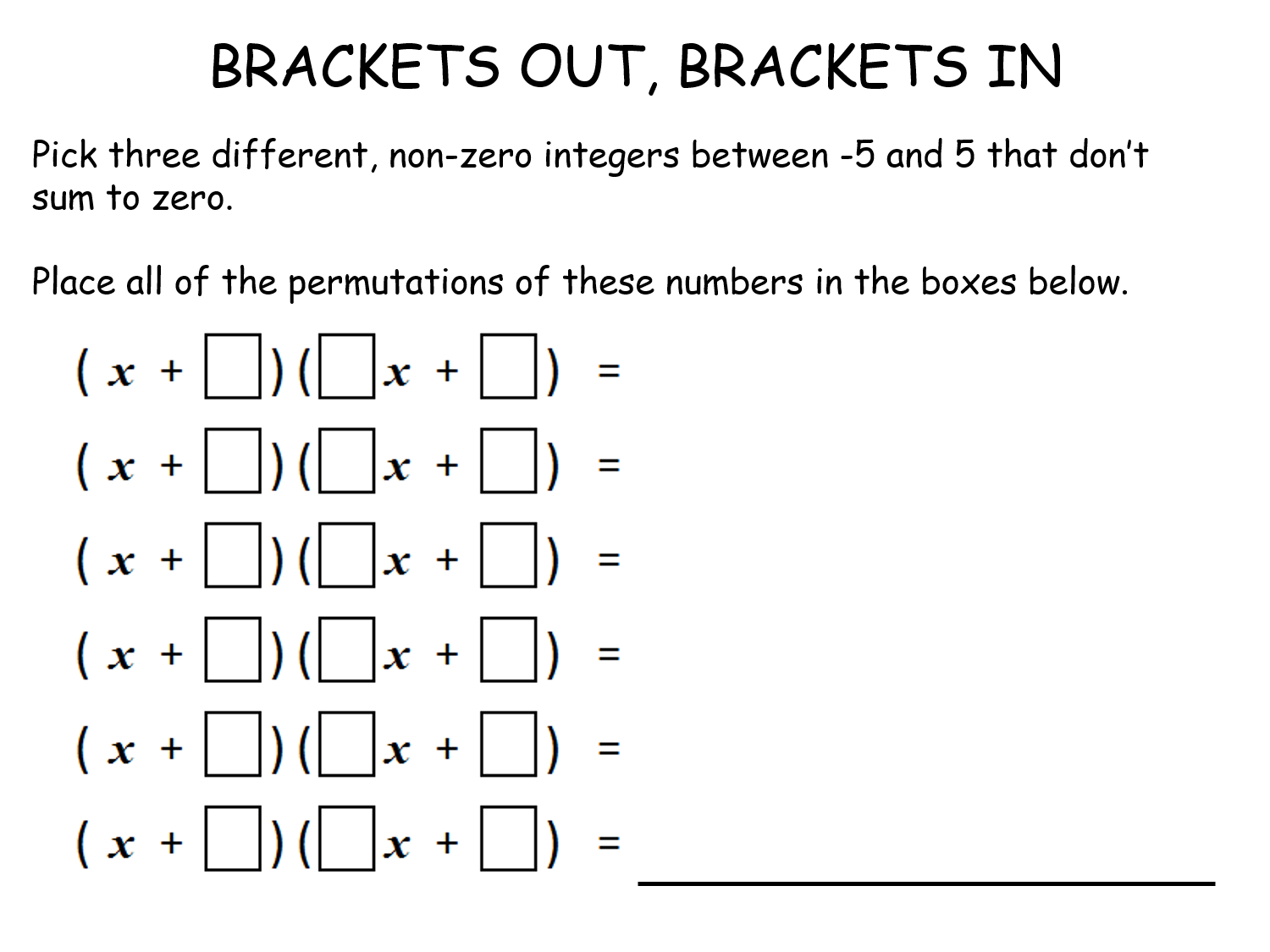
Brackets out, Brackets in |
RISP 3. Pupils have to simplify some algebra, that they have generated. All have the factor (x+1).Brackets out, Brackets in |
F
Year 1 - Pure
x_R_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Excel) (Excel) |
|
|
| 10 |
Magic Bag |
nRich. An algebra task thinly disguised as a probability question. The pupils have to determine the number of white balls in a bag. There are two answers! Triangular numbers are involved.Magic Bag |
H
Year 1 - Statistics
x_S_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 11 |
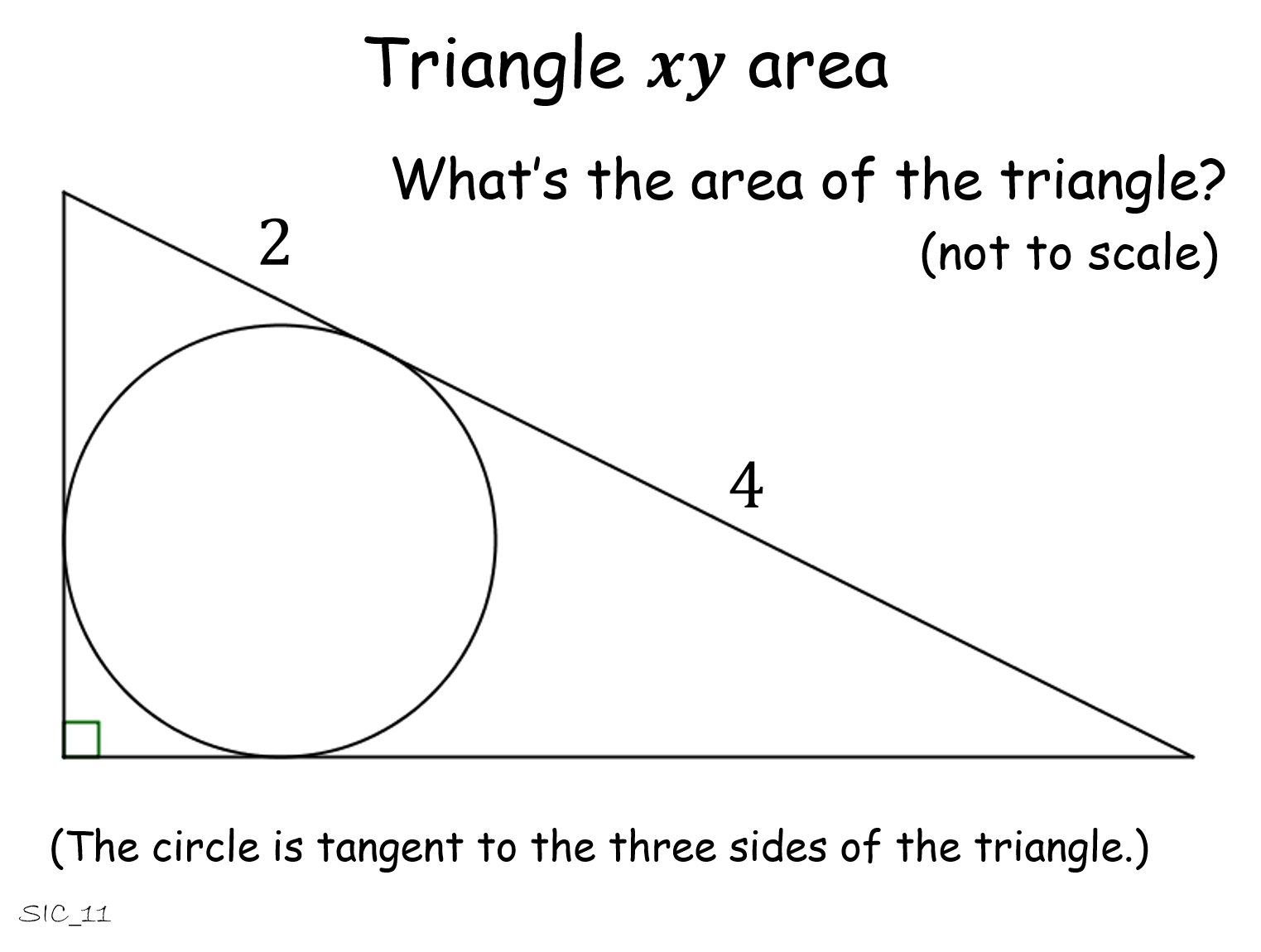
Triangle xy Area |
Work out the area of a triangle with an inscribed circle. Answers are all different but easily calculated from the given parameters.Triangle xy Area |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 12 |
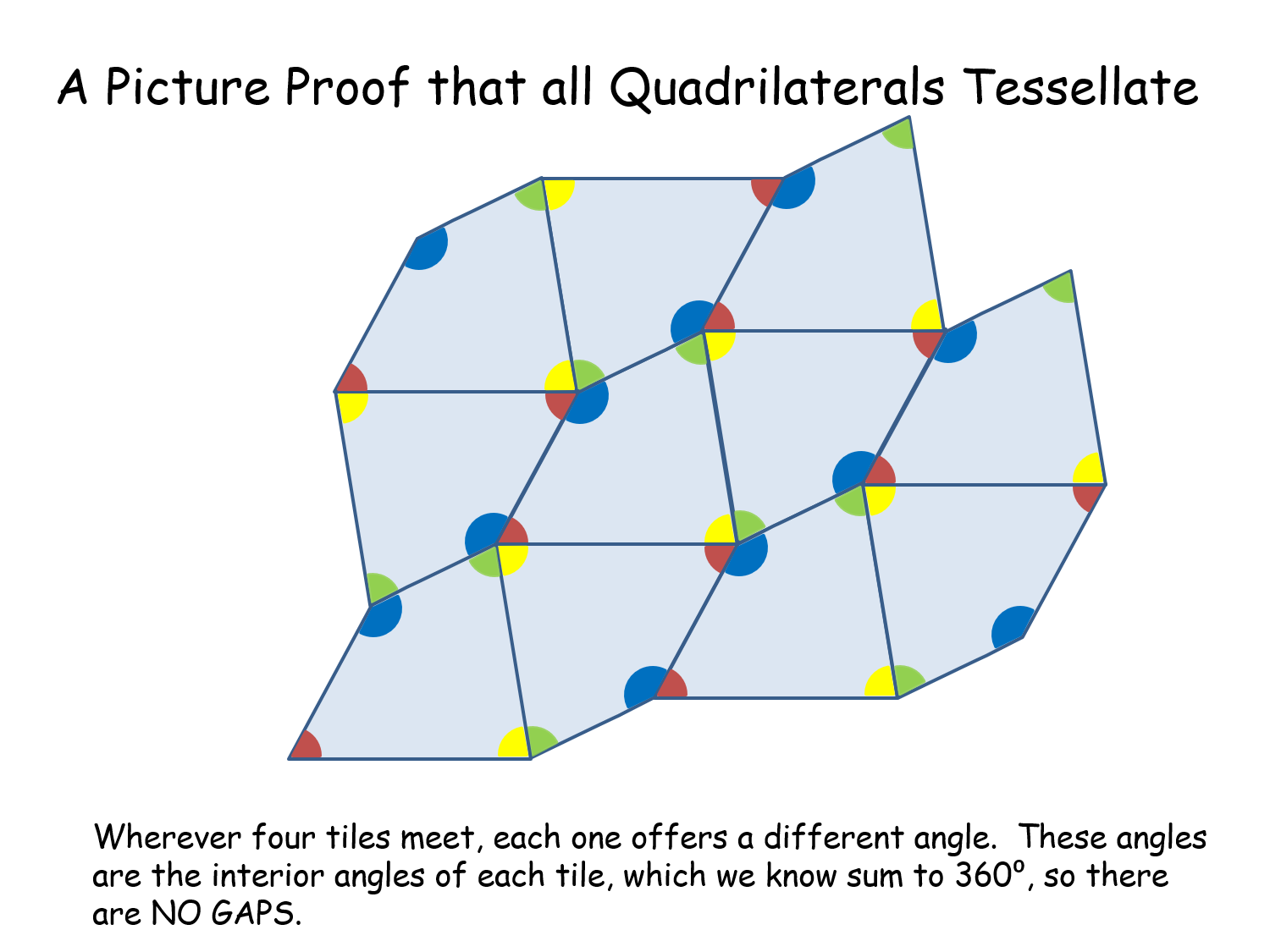
Quad Tessellate |
Get pupils to draw a quadrilateral that they think will not tessellate. Then reproduce it using the Geogebra file and show that it does. Then show a picture proof. No worksheet is required.Quad Tessellate |
A_
Year 7
x_A_x |
| |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
 (Geogebra) (Geogebra) |
|
| 13 |
A Geometric Progression Problem |
From clues given about the second and fourth terms of a geometric progression the pupils have to work out the possible solutions for the first term and common ratio.A Geometric Progression Problem |
F
Year 1 - Pure
x_R_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 14 |
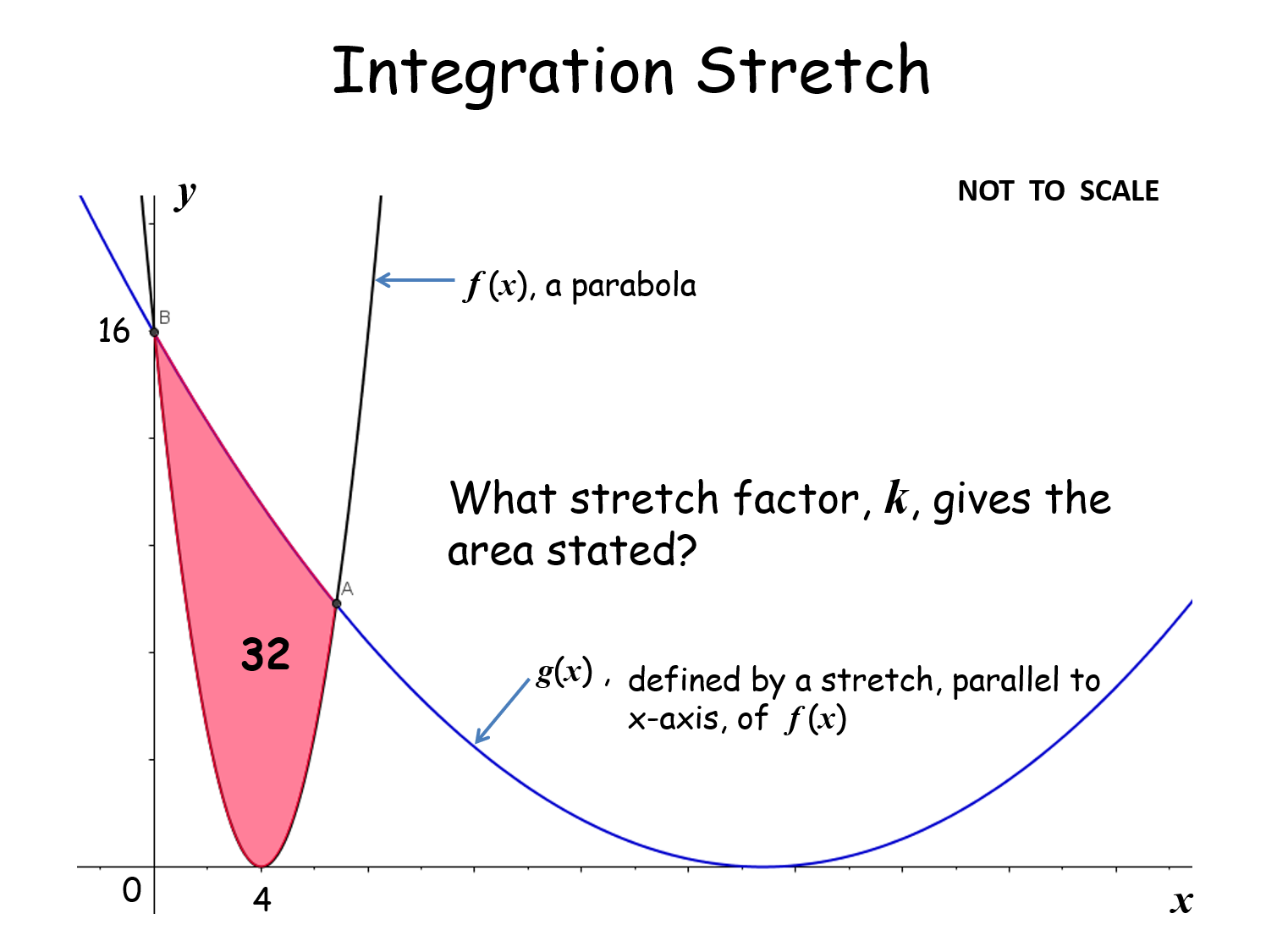
Integration Stretch |
A parabola is stretched - calculate the stretch factor to achieve the area bounded between the two. All parabolas are different but the stretch factors are the same.Integration Stretch |
J
Year 2 - Pure
x_T_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
 (Geogebra) (Geogebra) |
 (Adobe PDF) (Adobe PDF) |
| 15 |
Magic Fractions |
nRich. Using their own numbers (following a rule) the pupils form fractions and carry out operations on them. All answers are the same. No worksheet is required.Magic Fractions |
A_
Year 7
x_A_x |

| |
 (PowerPoint) (PowerPoint) |
|
|
|
| 16 |
Angle at Centre, Angle on Arc |
Discovery of two circle theorems. Pupils mark out angles on a chord and cut them out and compare.Angle at Centre, Angle on Arc |
D_
Year 10
x_D_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 17 |
Multi-Simultaneous |
Pupils are presented with a number of simultaneous equations to solve. How quickly will they spot that they only need to select one pair? How many will select the easiest pair rather than just the first two in the list?.......Multi-Simultaneous |
D_
Year 10
x_D_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Excel) (Excel) |
|
|
| 18 |
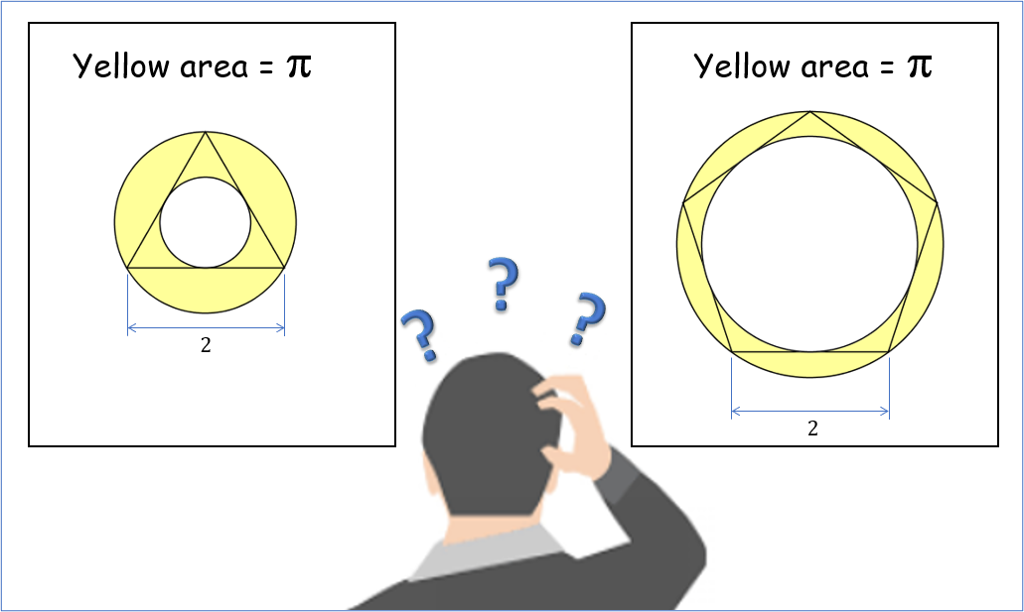
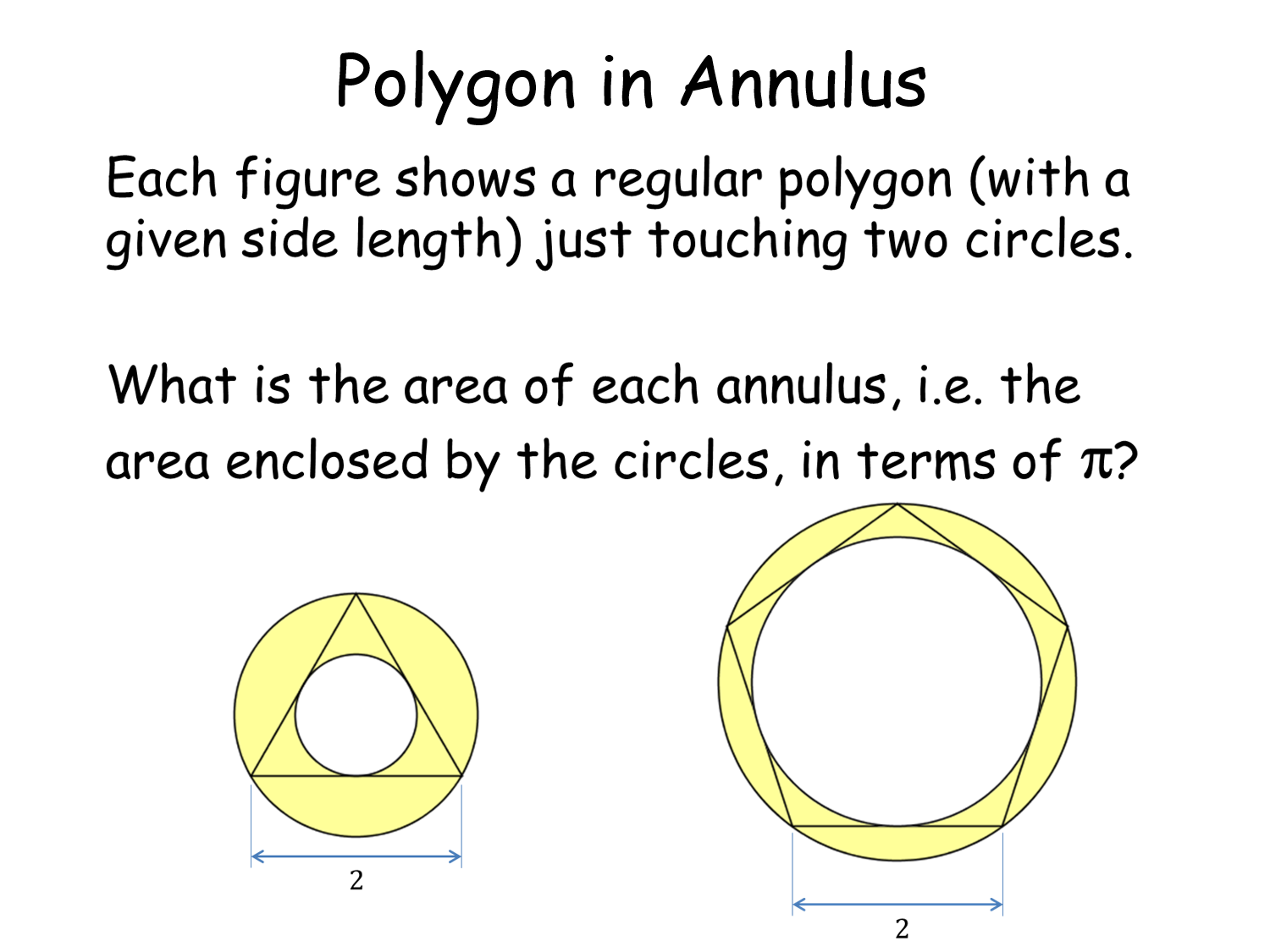
Polygon in Annulus |
Pupils need to work out the area of a couple of rings with different dimensions - but the same area.Polygon in Annulus |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 19 |
Cubic Tangent Circle |
Pupils need to work out the equation of a cubic and draw a tangent at a specific place. All tangents should go through the first root.Cubic Tangent Circle |
F
Year 1 - Pure
x_R_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 20 |
Hyper Parabola |
Pupils need to find out where a parabola and a hyperbola just touch. This activity reinforces the notion of double roots and discriminant = 0.Hyper Parabola |
F
Year 1 - Pure
x_R_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 21 |
Leonardo of Pisa |
Pupils are given the nth term of a sequence and are asked to find specific (non consecutive) terms in the sequence. It is the Fibonacci sequence. The task involves surds and indices. Then they are asked to prove that the ratio of consecutive terms tends to the golden ratio.Leonardo of Pisa |
D_
Year 10
x_D_x |
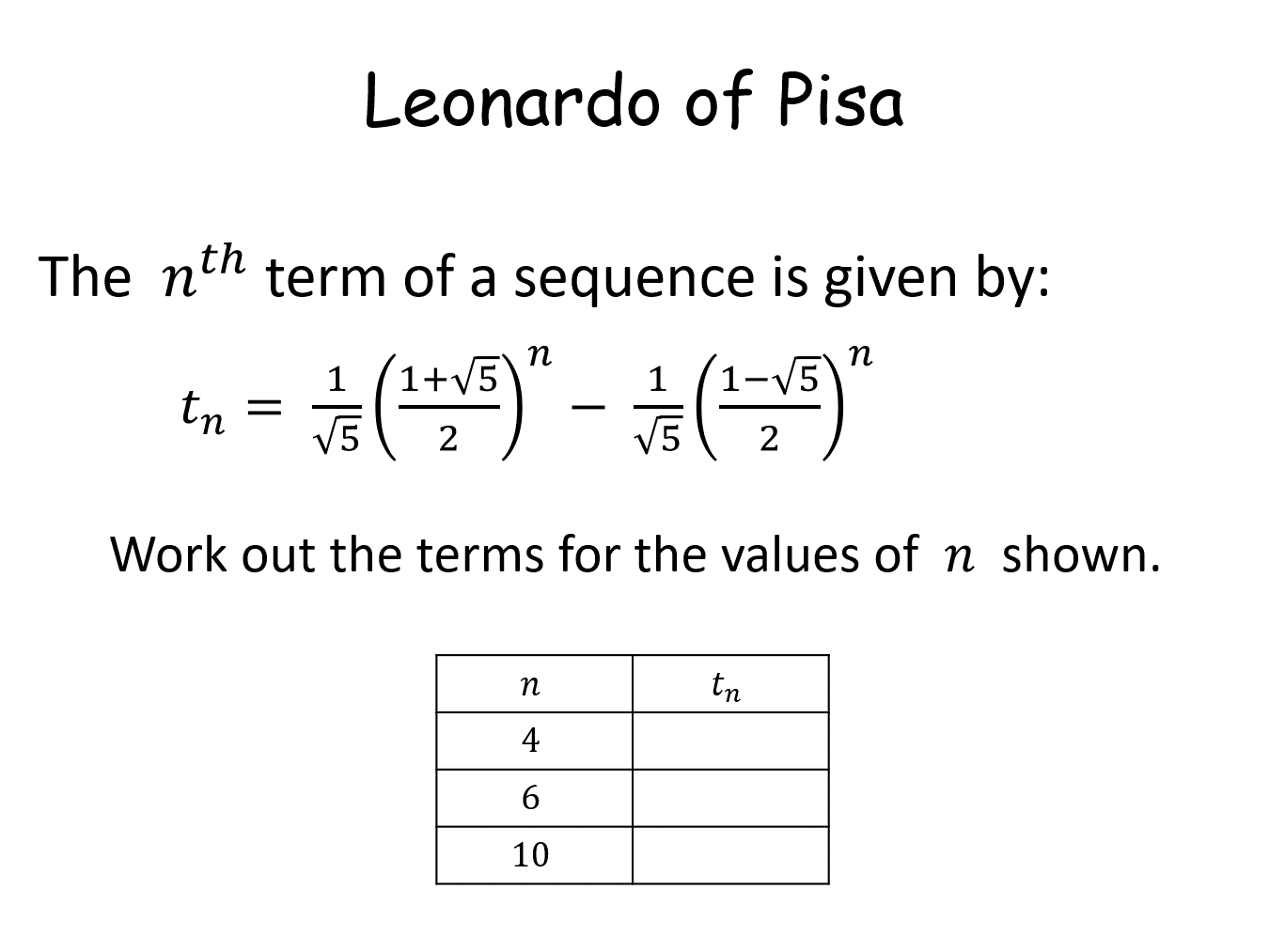
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Excel) (Excel) |
|
|
| 22 |
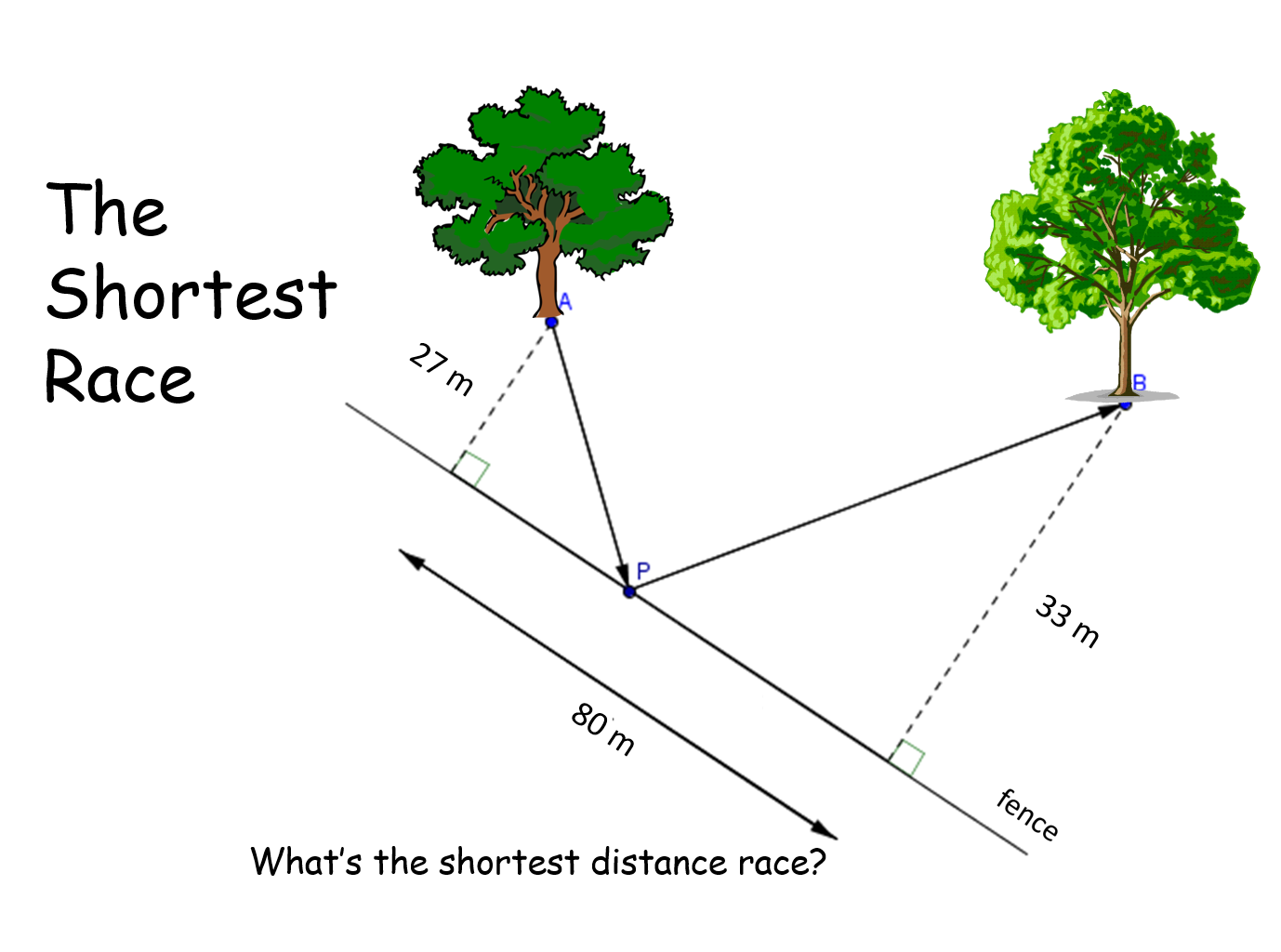
The Shortest Race |
You have to run from tree A to tree B whilst touching a fence. Where should you touch the fence to minimise the distance you have to run?The Shortest Race |
J
Year 2 - Pure
x_T_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 23 |
A Fractional Sequence |
An inductive formula is given with each pupil having different starting values. They have to find the 11th and 12th terms. The sequence loops (but they don't know that) so they don't need to go that far. Then, of course, they have to prove it always loops!A Fractional Sequence |
F
Year 1 - Pure
x_R_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 24 |
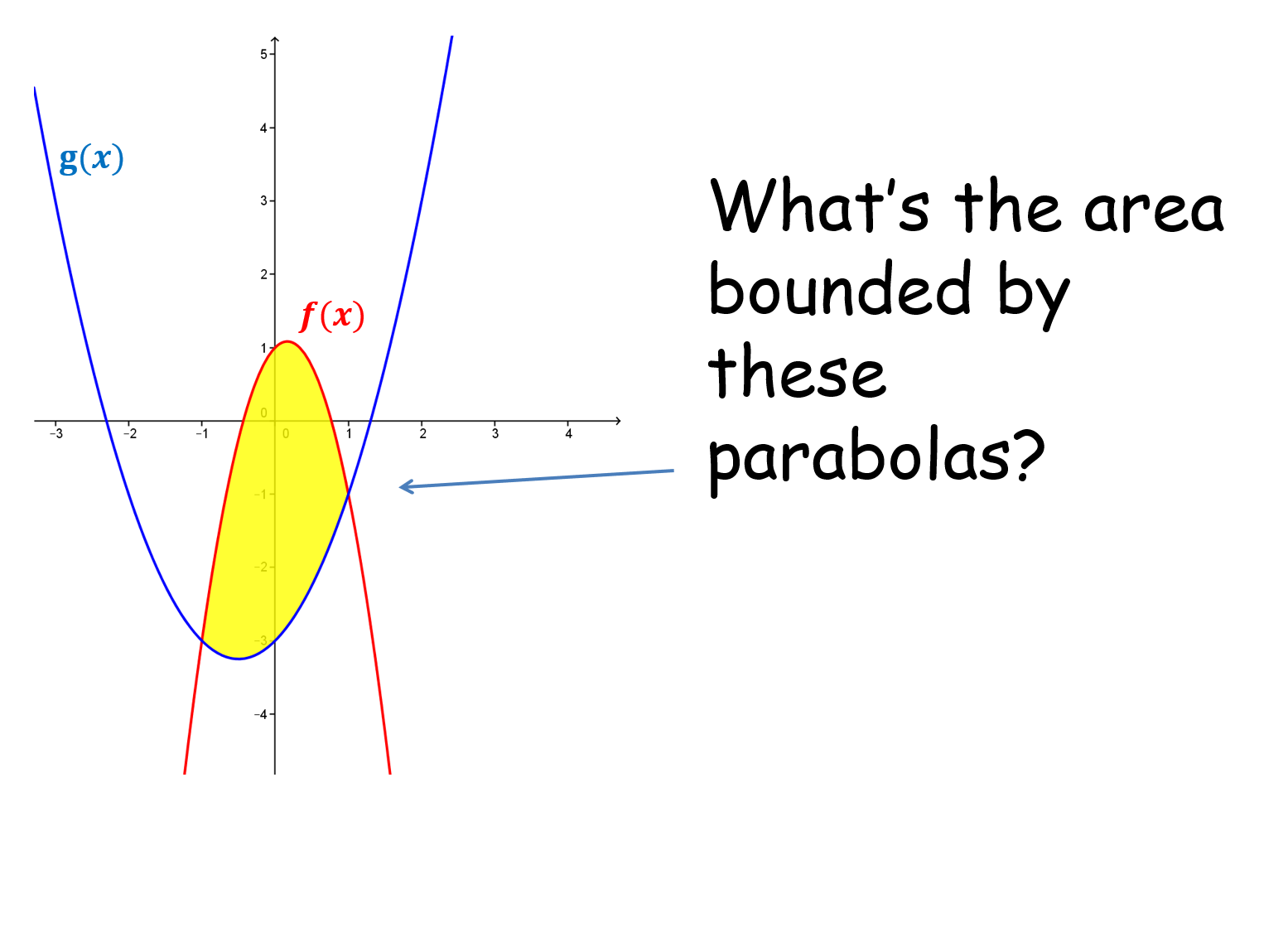
Area between Parabolas |
An integration activity around the area bounded by two parpabolas. Some pupils are confused if the area straddles the x-axis. This activity adresses this.Area between Parabolas |
F
Year 1 - Pure
x_R_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 25 |
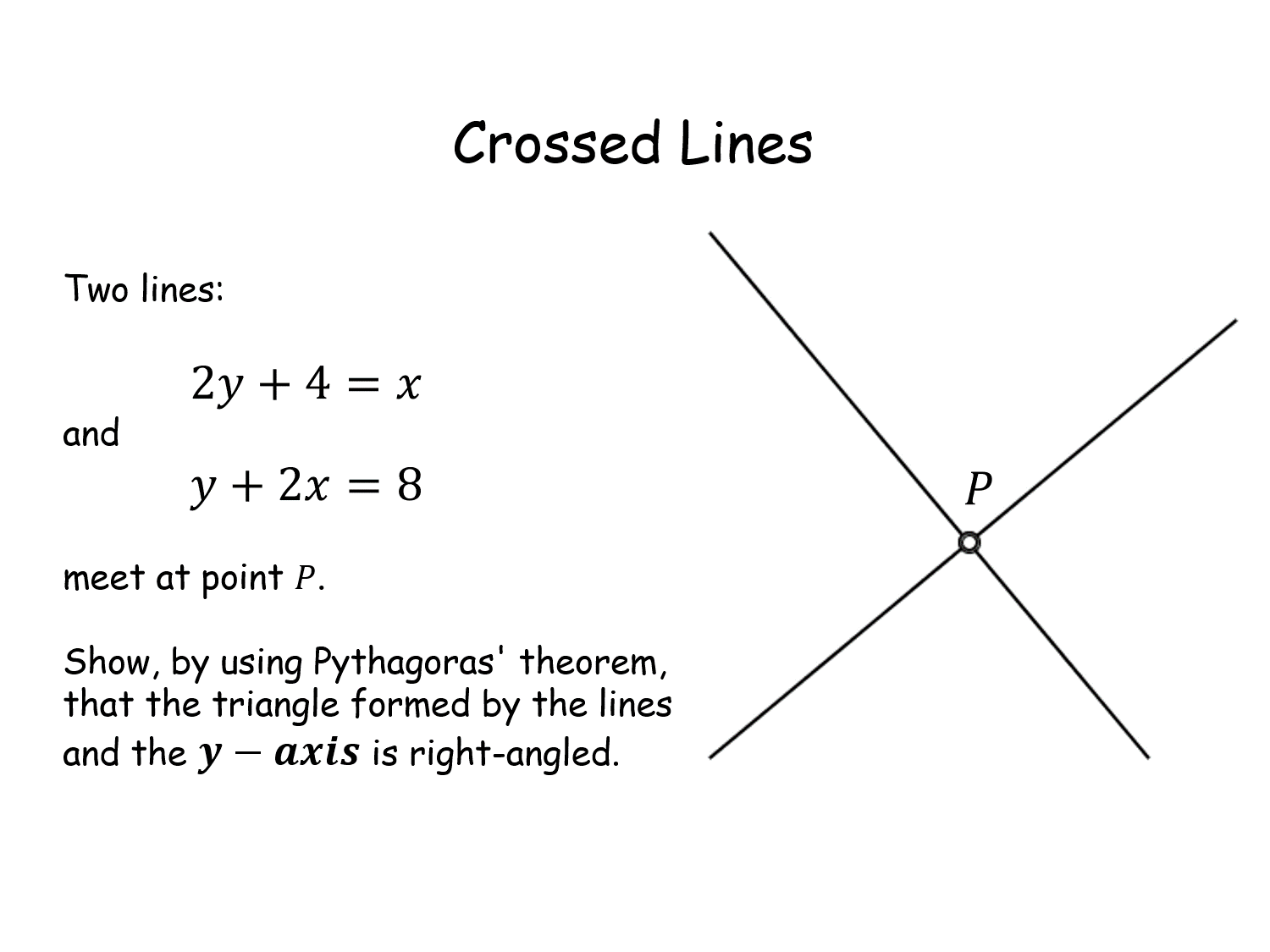
Crossed Lines |
This tests the pupils' knowledge of straight line graphs and y=mx+c and the significance of gradients of perpendicular lines.Crossed Lines |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 26 |
Shoot the Monkey |
Projectiles. You want to shoot a monkey hanging in a tree. But he's a cheeky monkey and at the exact moment you fire, he lets go and falls to the ground. Knowing this, where should you aim to be sure of hitting your target?Shoot the Monkey |
K
Year 2 - Mechanics
x_U_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 27 |
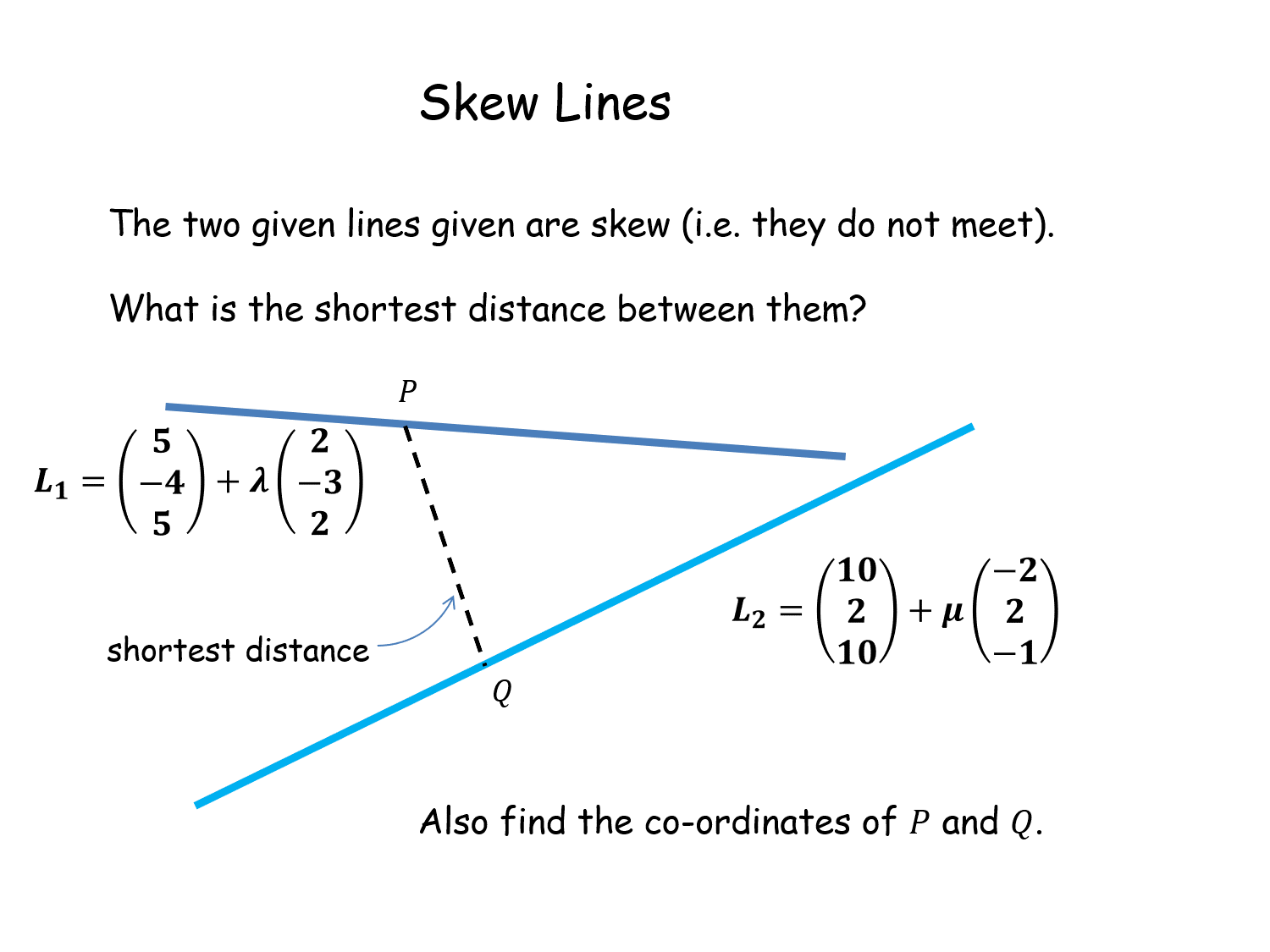
Skew Lines |
Skew lines in 3D space in vector form. How close do they get?Skew Lines |
J
Year 2 - Pure
x_T_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 28 |
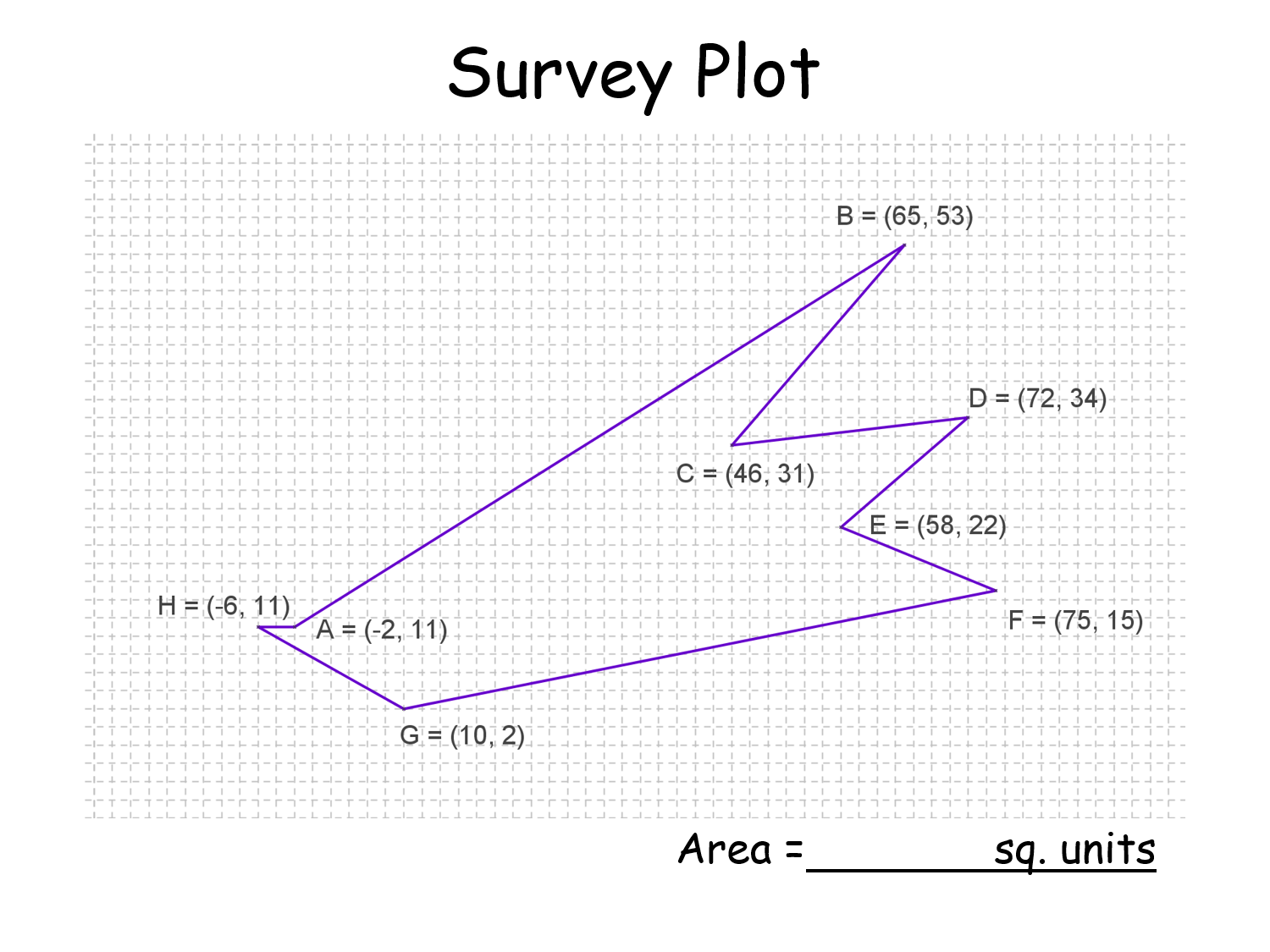
Survey Plot |
Imagine you needed to remove one metre depth of topsoil from a new building plot. What volume does this represent? How many wagons will you need, etc? By approximating this area to a polygon (where you know the coordinates of the vertices) makes the task very easy (even easier with a spreadsheet).Survey Plot |
F
Year 1 - Pure
x_R_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Excel) (Excel) |
 (Geogebra) (Geogebra) |
|
| 29 |
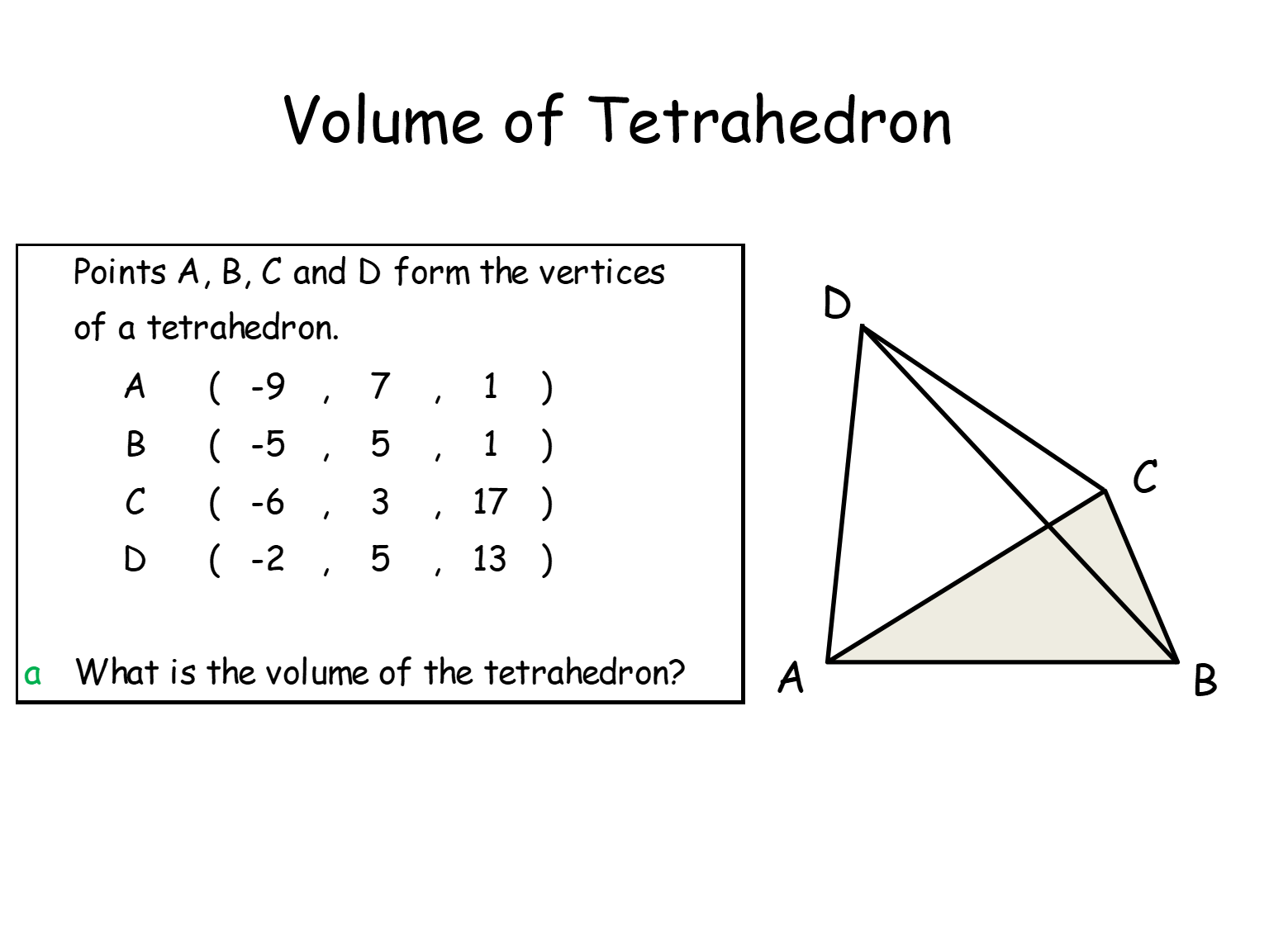
Volume of Tetrahedron |
Given the 3D coordinates of four points what is the volume of the tetrahedron that is formed by joining them with line segments? This brings together just about everything they need to know about vectors and so is a good revision task. The solution does not use the triple product. All the volumes are the same.Volume of Tetrahedron |
J
Year 2 - Pure
x_T_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Excel) (Excel) |
 (Autograph) (Autograph) |
 (Autograph) (Autograph) |
| 30 |
Parabola in Parallelogram |
Given certain facts about a parabola the pupils have to determine its equation. Then they need to integrate the function to work out ratios of areas. There is a neat solution that makes it very easy to do - which you can show them at the end. A further extension is to challenge them to do it without integration.Parabola in Parallelogram |
F
Year 1 - Pure
x_R_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Excel) (Excel) |
|
|
| 31 |
Straight Line |
A very simple (but illuminating) task where pupils follow simple instructions and generate the equation of a straight line from consideration of areas of triangles. Each equation is different but easy for the teacher to ascertain the answer by visual inspection.Straight Line |
B_
Year 8
x_B_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 32 |
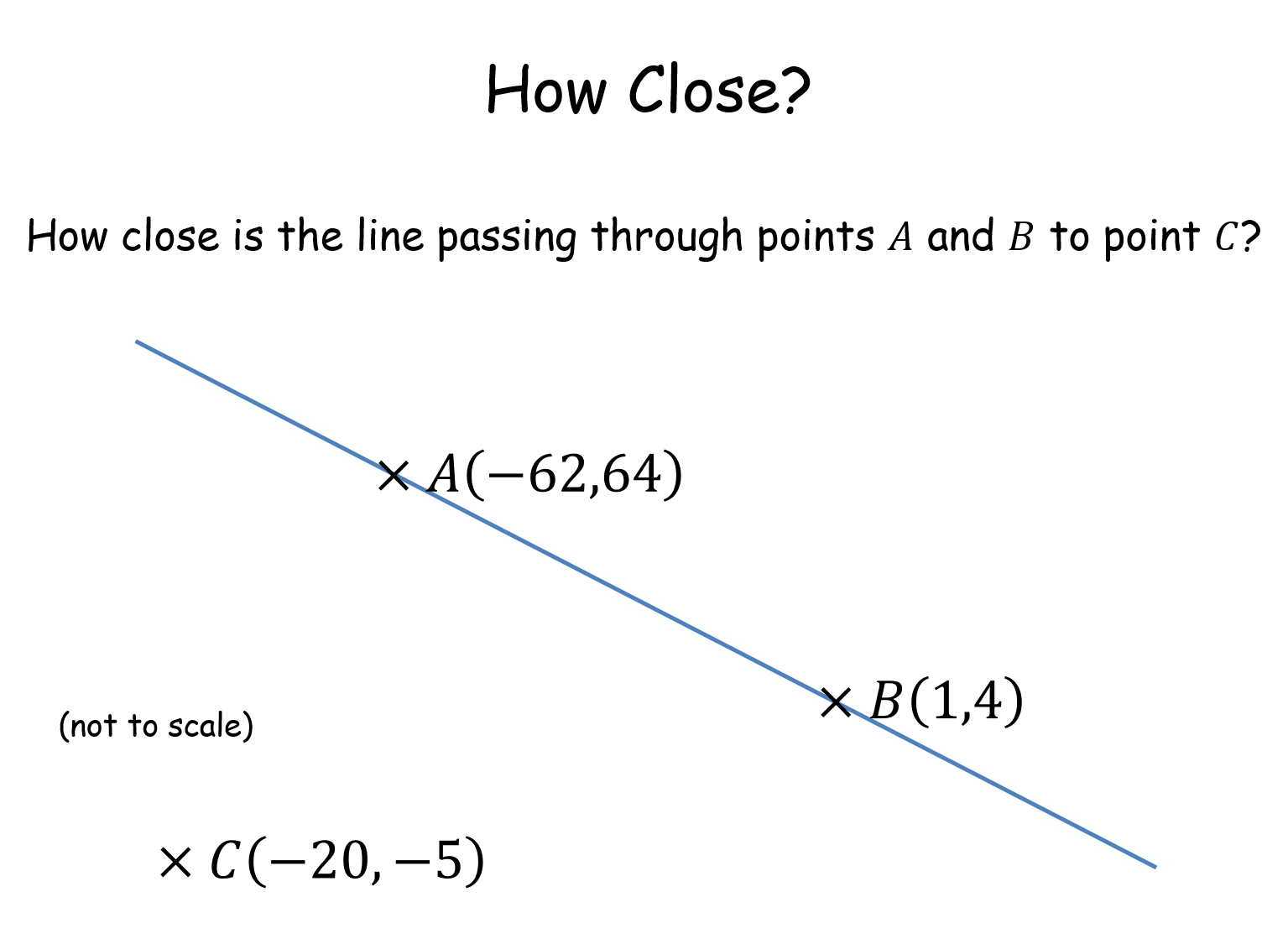
How Close? |
A coordinate geometry task. Pupils have the coordinates of two points on a line. How close is this line to a third point? All pairs of coordinates are different but lie on three different lines - but the closest distance is the same for all.How Close? |
F
Year 1 - Pure
x_R_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 33 |
Target Range |
Simple projectiles problem. Given two points on a trajectory the pupils need to ascertain range, angle of elevation and muzzle velocity. A good test to see if they can remember how to do it from first principles.Target Range |
K
Year 2 - Mechanics
x_U_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 34 |
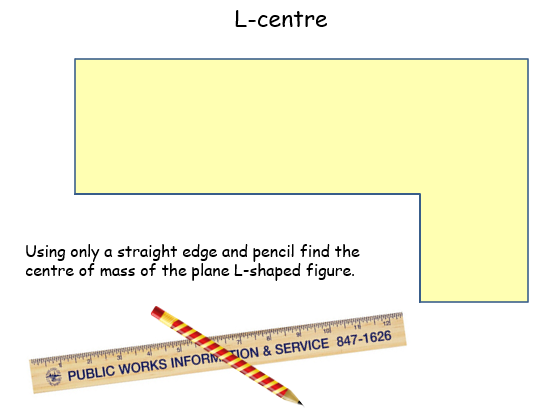
L-centre |
Hands-on activity to find the centre of mass of an L-shaped plane figure by construction only. But there is something special about them all - each centre of mass is at the inner elbow of the L. Can the pupils work out why this is? The golden ratio is involved.L-centre |
N
Year 2 - Further Mechanics
x_U_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 35 |
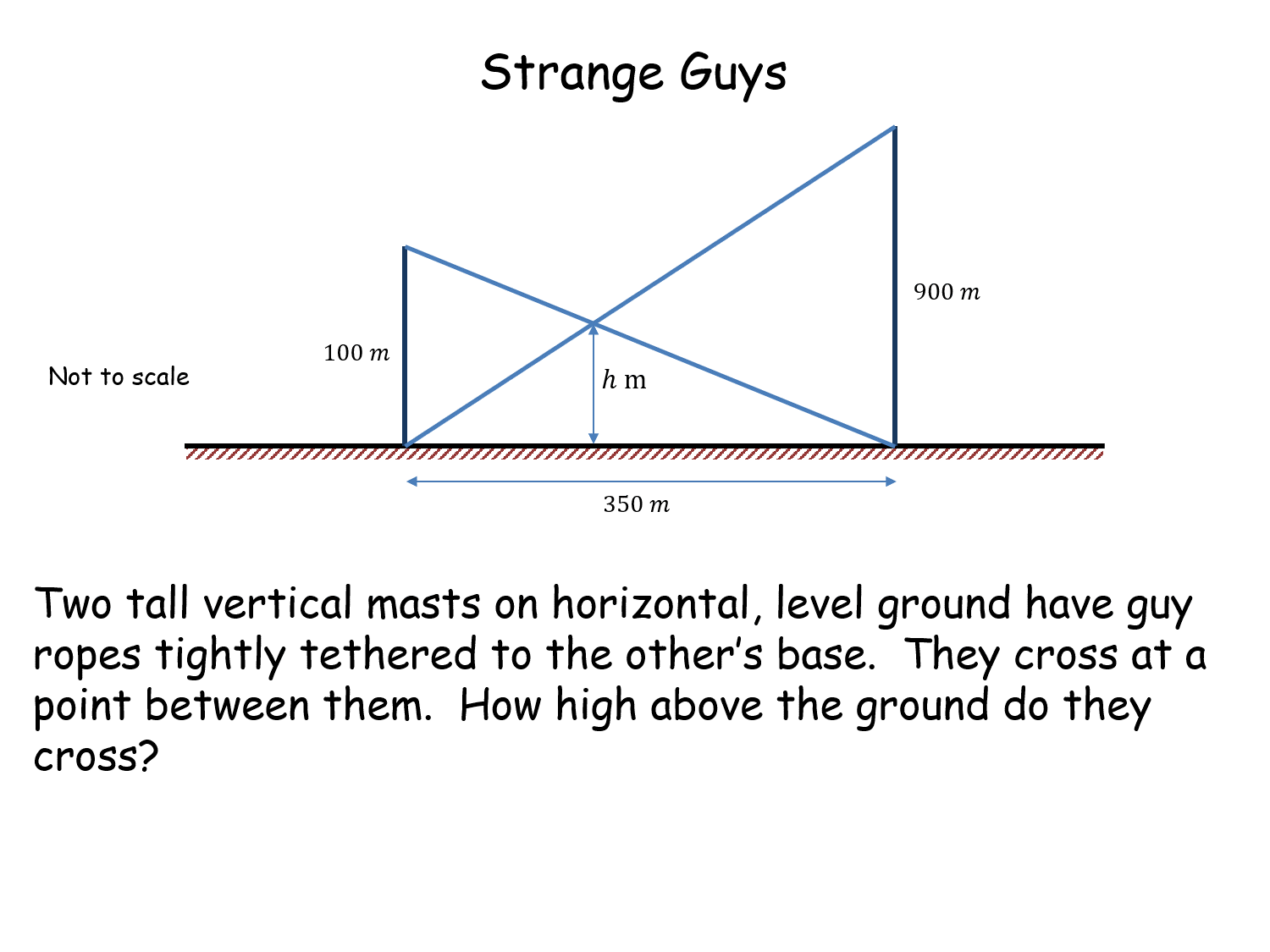
Strange Guys |
Classic problem involving masts and guy ropes solved using the application of similar triangles. The activity brings out the fact that the distance between the masts is irrelelvant to the question posed. All the answers are the same (90 m). Strange Guys |
C_
Year 9
x_C_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 36 |
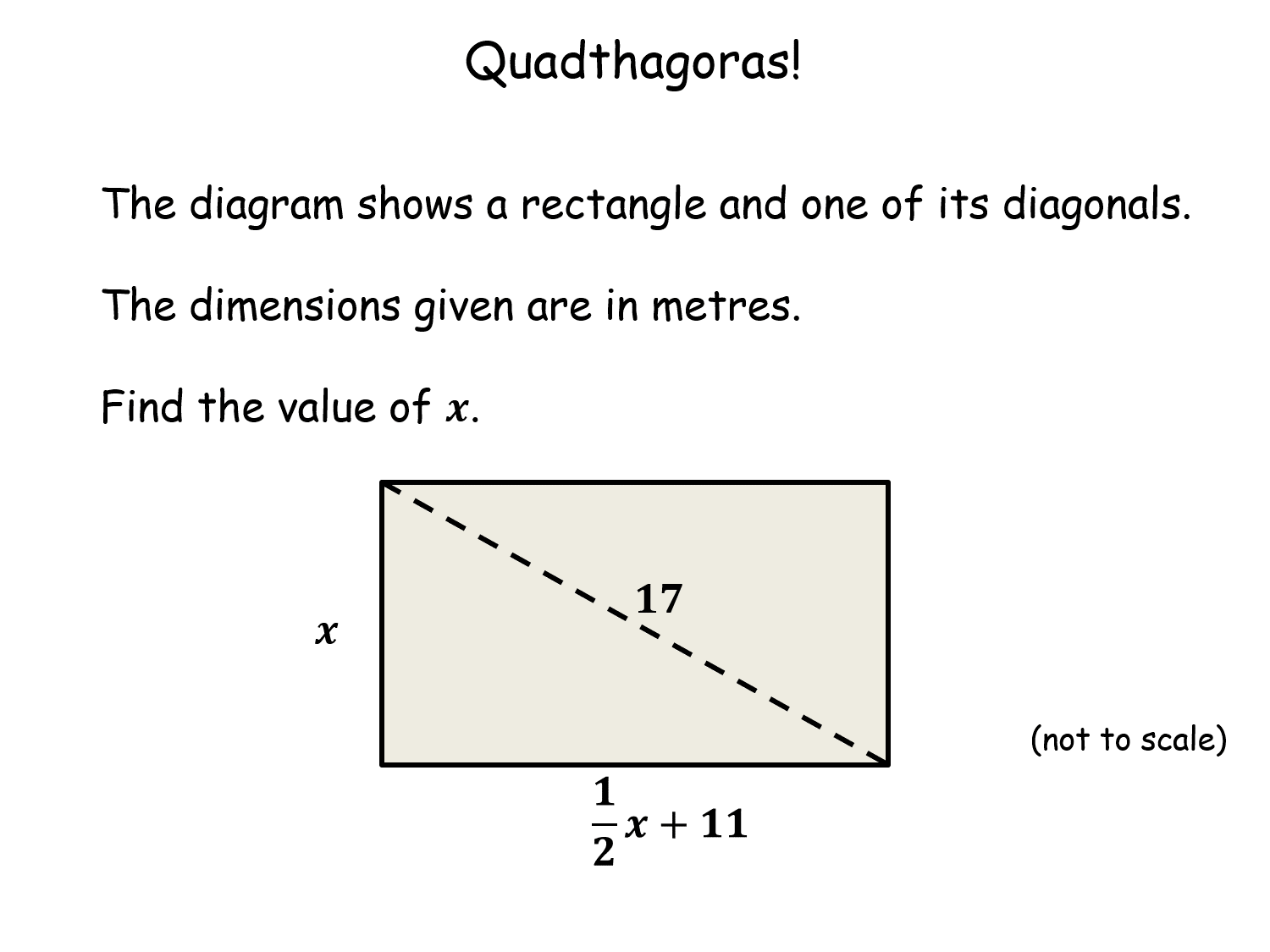
Quadthagoras! |
Problem involving forming and solving a quadratic equation. Conceptually not very hard but pupils will need knowledge of the quadratic formula, because although all of the quadratics can be factorised they can be tricky due to coefficients greater than 1. Can the pupils work out how all the answers are the same?Quadthagoras! |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 37 |
Find f(2) |
A slightly cryptic question based on a quadratic function. Not too difficult but a little different from the norm. As an extension you could ask the pupils to come up with their own parameters that give the same solution.Find f(2) |
F
Year 1 - Pure
x_R_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 38 |
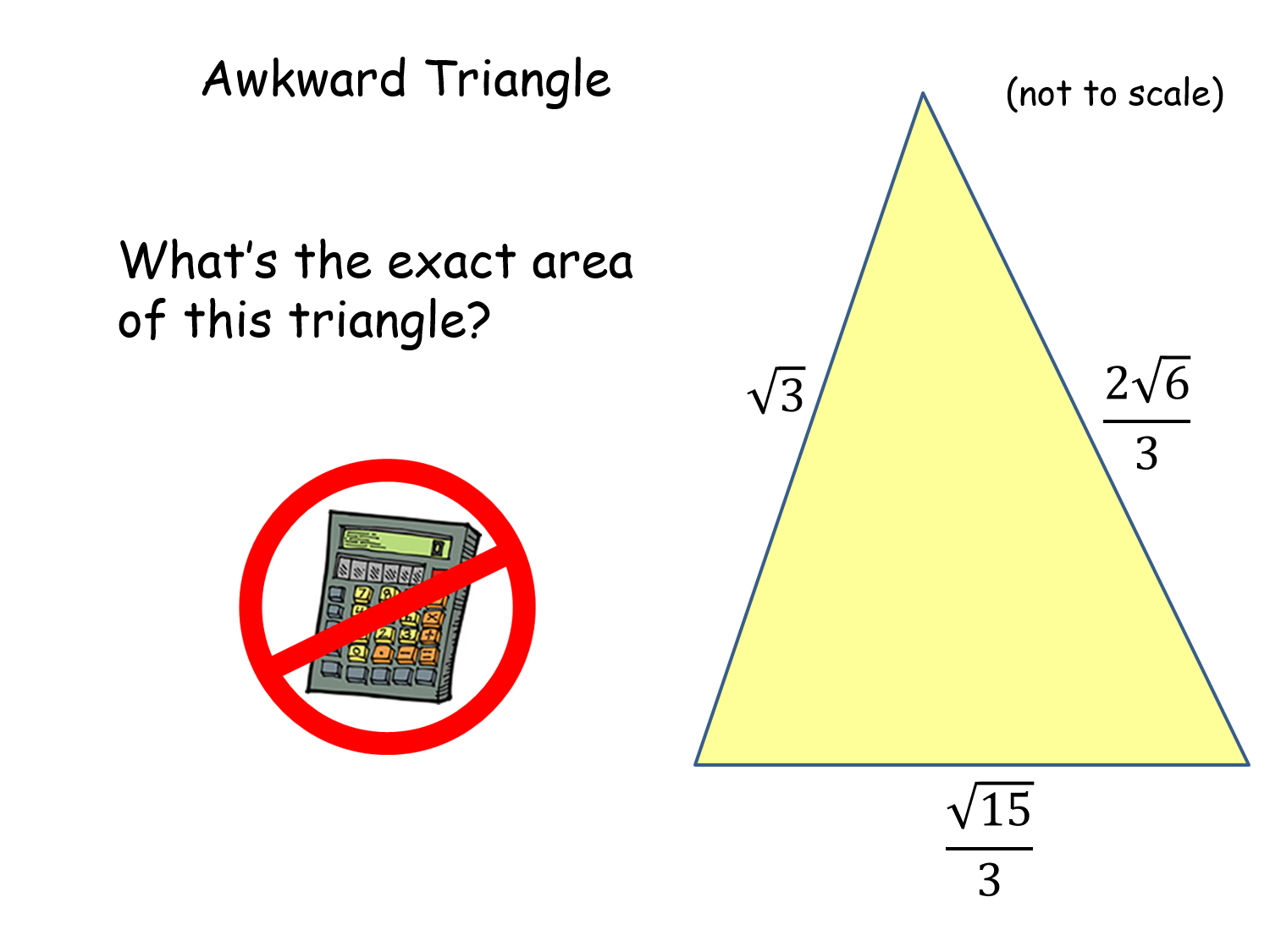
Awkward Triangle |
Given the side lengths of a scalene triangle (in surd form) can the pupils work out its area? Tests use of the Cosine Rule and multiplication and simplification of surds. For interest, Heron's formula is also used to solve the problem.Awkward Triangle |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 39 |
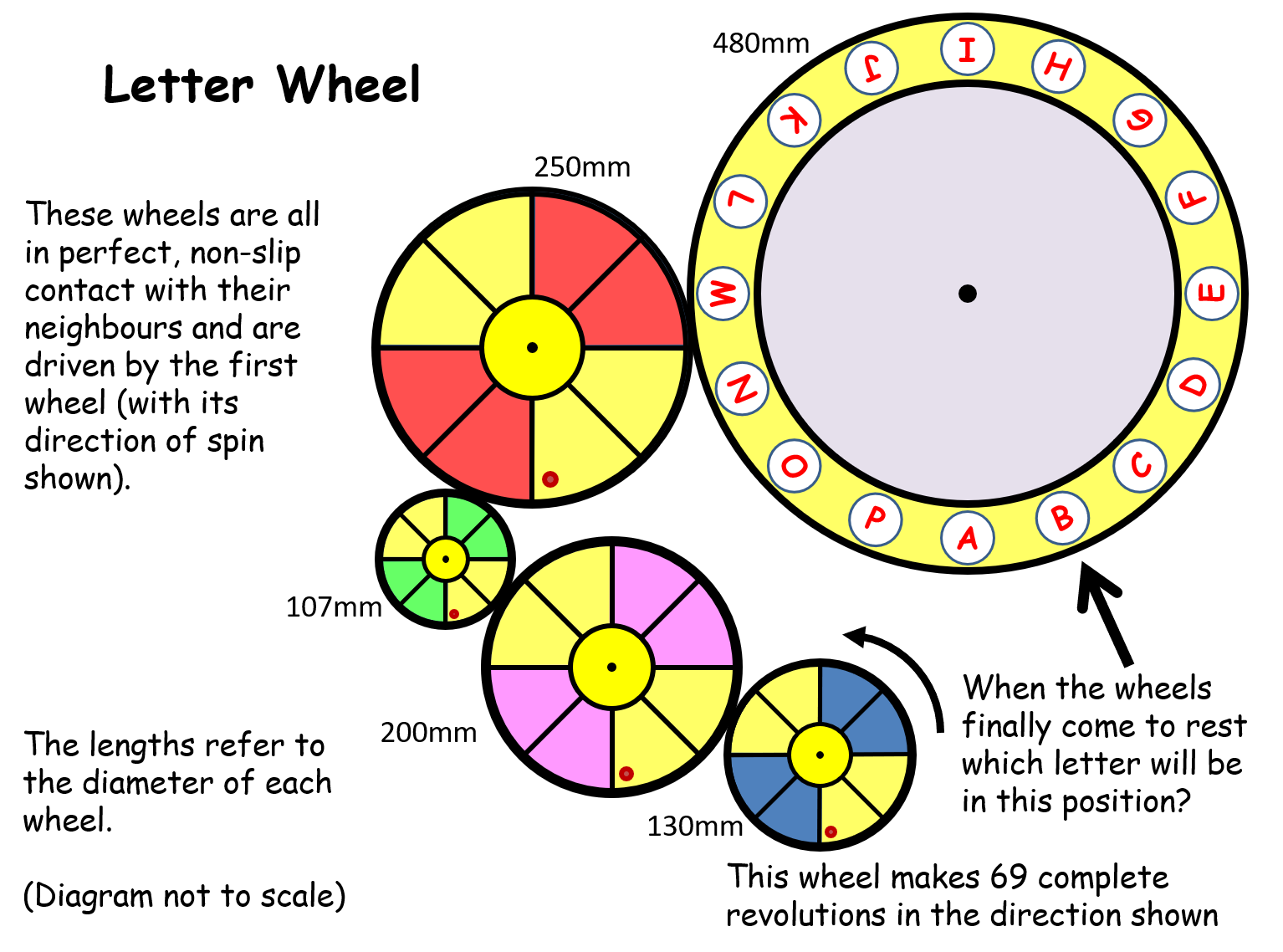
Letter Wheel |
Pupils have to work out how much the last wheel of five connected wheels turns when told how much the first wheel turns. Sixteen different answers but teacher knows each answer from information coded in the worksheeet. Can introduce modulo arithmetic.Letter Wheel |
B_
Year 8
x_B_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Scratch) (Scratch) |
|
|
| 40 |
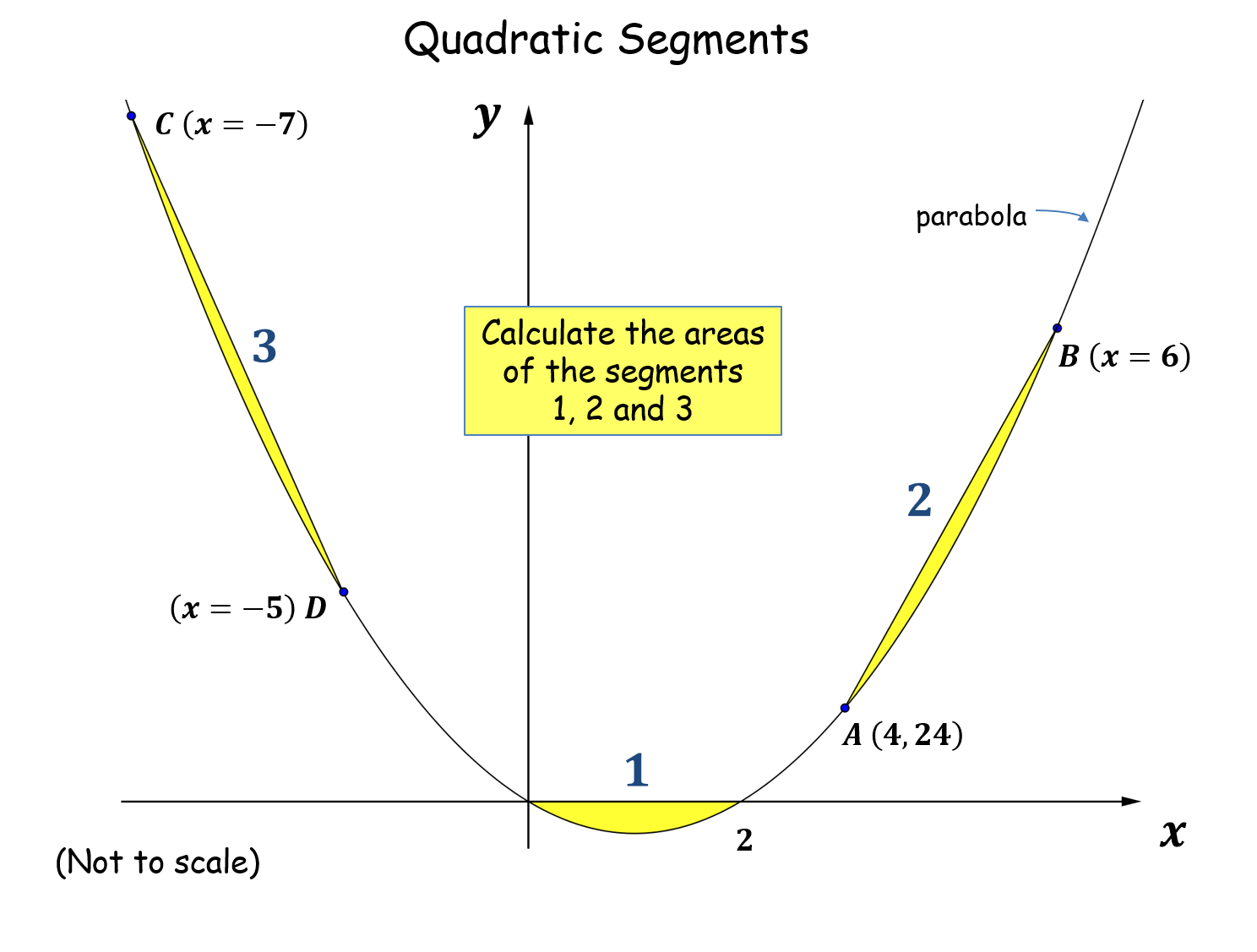
Quadratic Segments |
Pupils have to work out the area of three segments formed by chords of equal horizontal widths drawn on a parabola. Interestingly, this area is invariant for a given width. They discover this and then hopefully prove it.Quadratic Segments |
J
Year 2 - Pure
x_T_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 41 |
Cross Bear! |
Three bears start scoffing porridge at different rates and then start scoffing each other's. Pupils have to work out the individual rates. Teacher can find the answer encoded in the worksheeet by multiplying a number by 10.Cross Bear! |
C_
Year 9
x_C_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 42 |
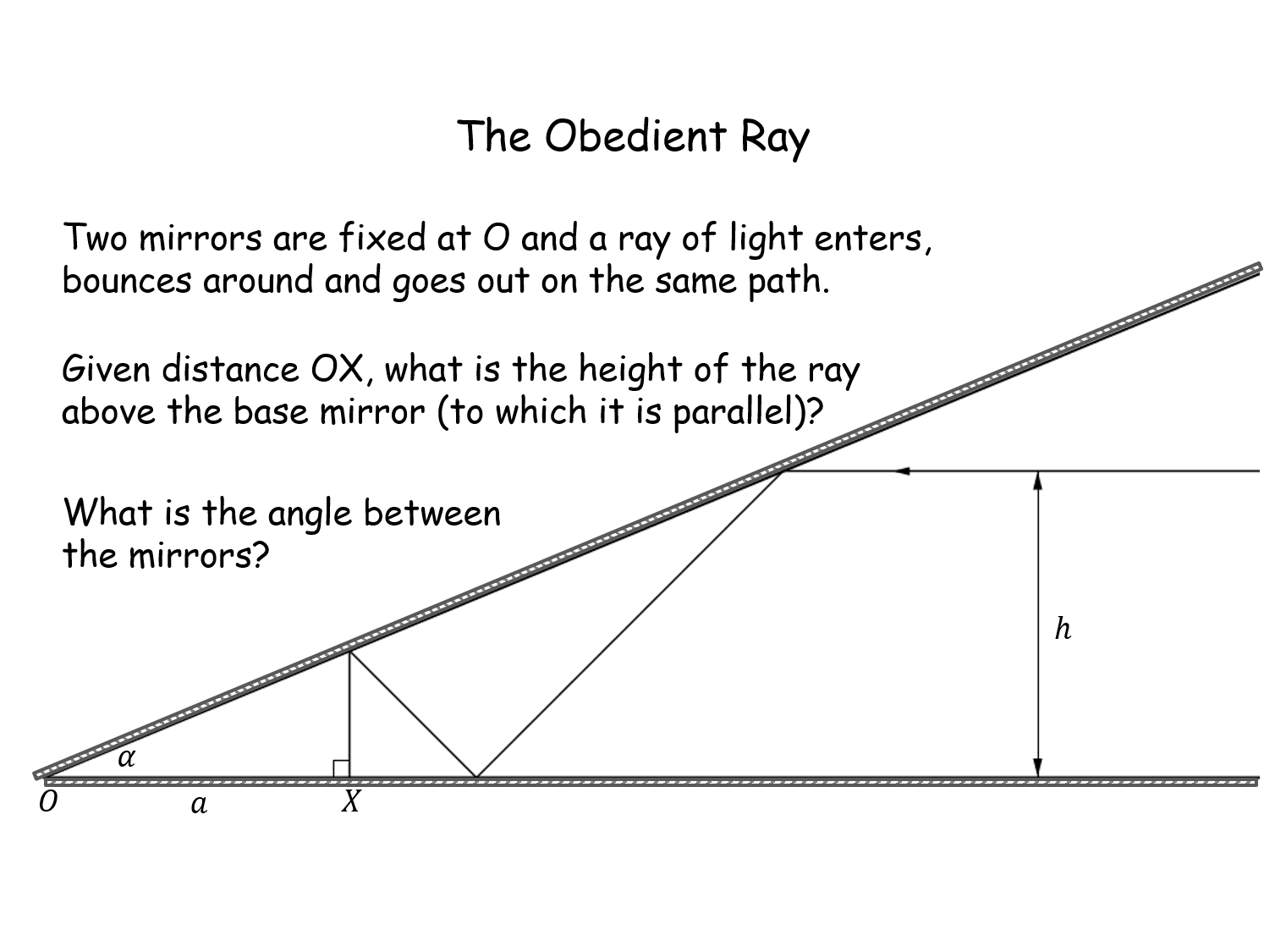
The Obedient Ray |
A light ray bounces between two mirrors and retraces its steps. The angle (to be determined) between the mirrors is the same but the height of each ray is different. Simple geometry yields the answer but pupils are invited to look at a more general case. Pupils may not know about the law of reflection but it is not a great stretch of the imagination.The Obedient Ray |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 43 |
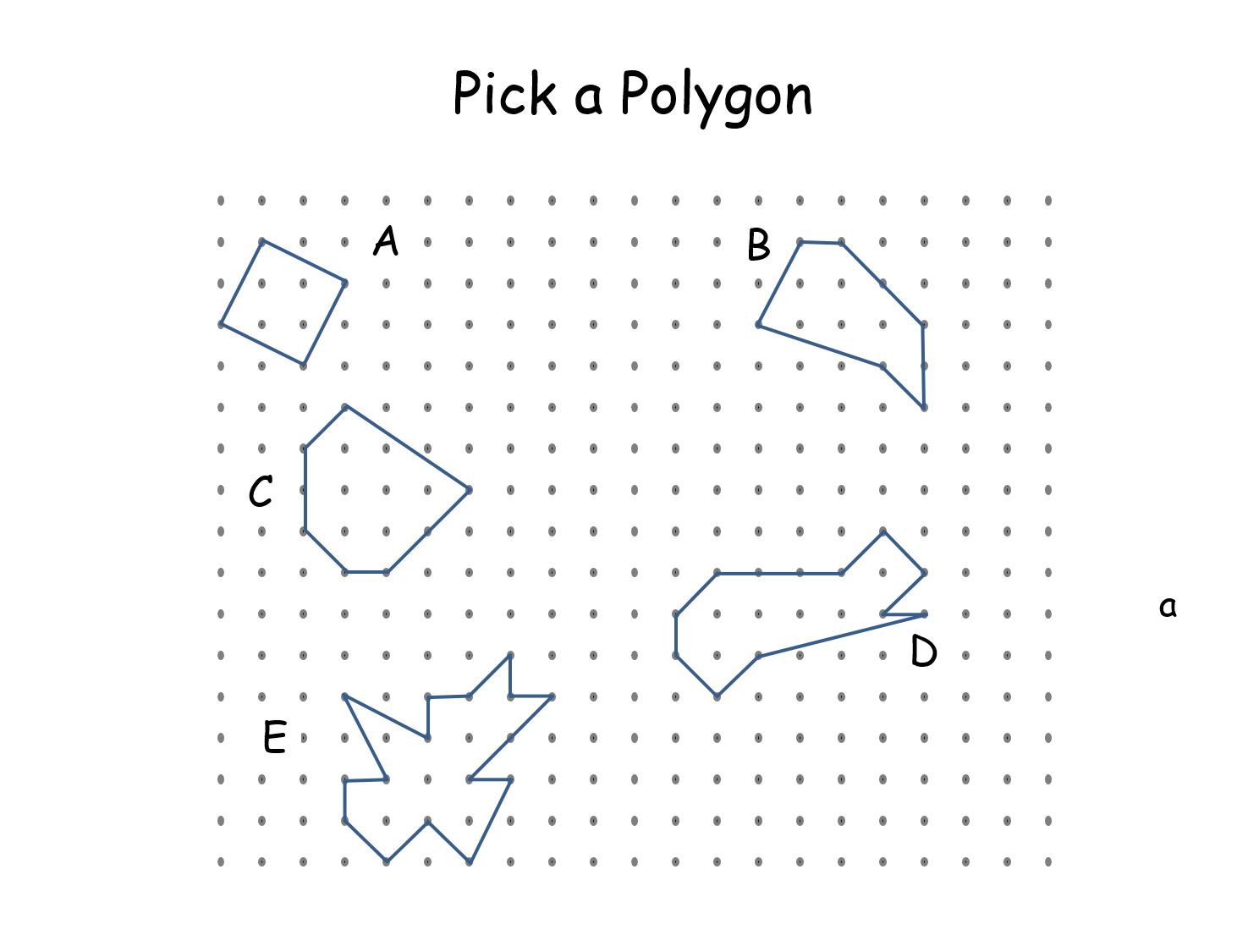
Pick a Polygon |
Pupils discover Pick's Theorem. Each worksheet has different polygons but polygons allocated to a given letter have the same area. They are invited to draw more polygons and discover the formula for the area.Pick a Polygon |
B_
Year 8
x_B_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Word) (Word) |
|
|
| 44 |
Sea Shell Product |
Pupils discover an intriguing result - the product of the lengths of the chords equals the number of equally spaced dots on the circle. Quite simple trigonometry and lengths of sides of triangles involving surds. The proof of the result will be beyond them. See task no. 84, aimed at Further Mathematicians, for the proof.Sea Shell Product |
D_
Year 10
x_D_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 45 |
Piscatorial Percentages |
A counter-intuitive result involving percentages. It's a nice little problem to solve algebraically but there is also a very simple way to do it which makes it even more worth doing. I couldn't resist using some Escher artwork.Piscatorial Percentages |
C_
Year 9
x_C_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 46 |
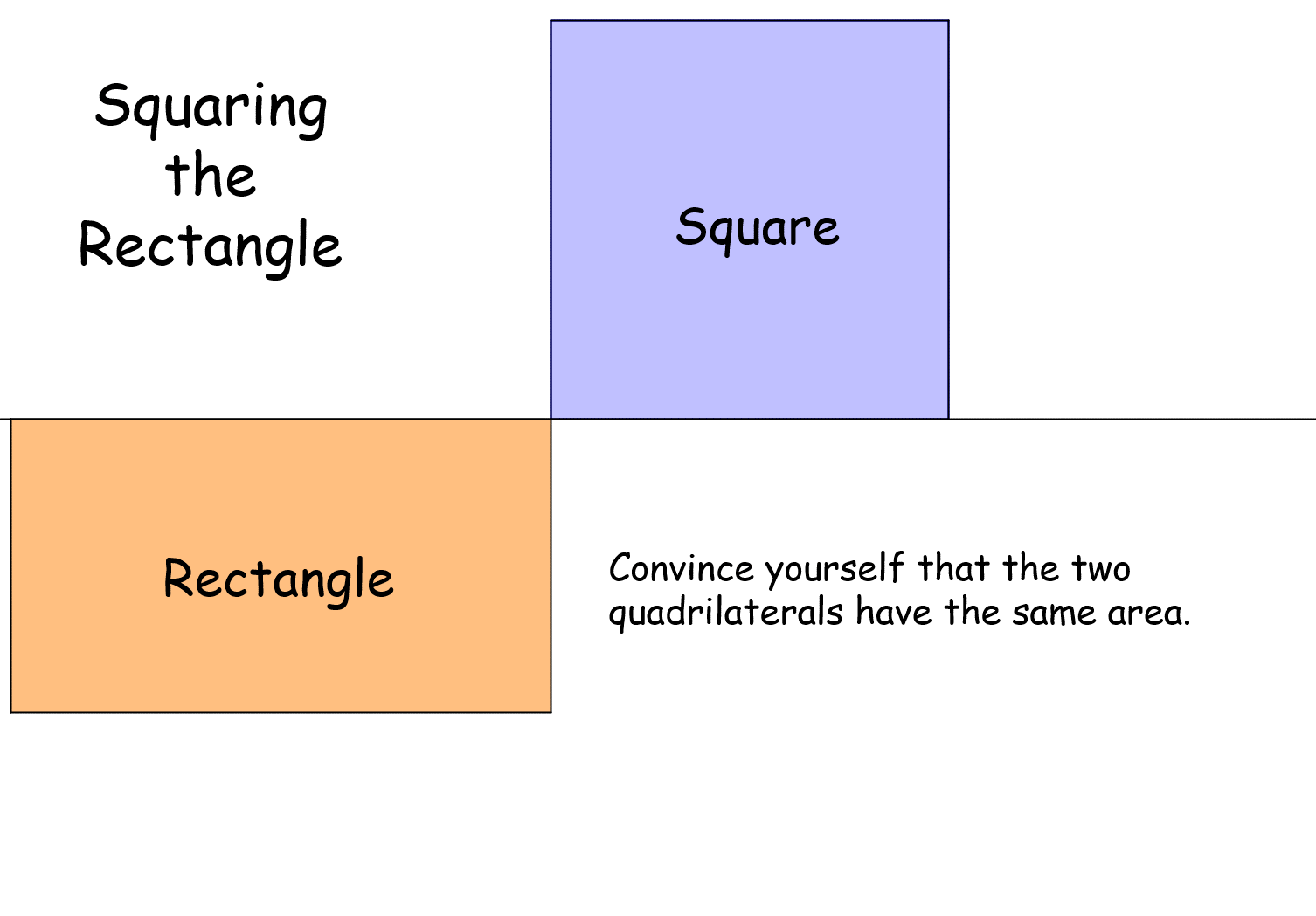
Squaring the Rectangle |
Pupils are asked to construct a square with area equal to a given rectangle, using construction methods only. Gives practice in constructions and application of the intersecting chords theorem. Leads to determining the square root of a number by construction.Squaring the Rectangle |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 47 |
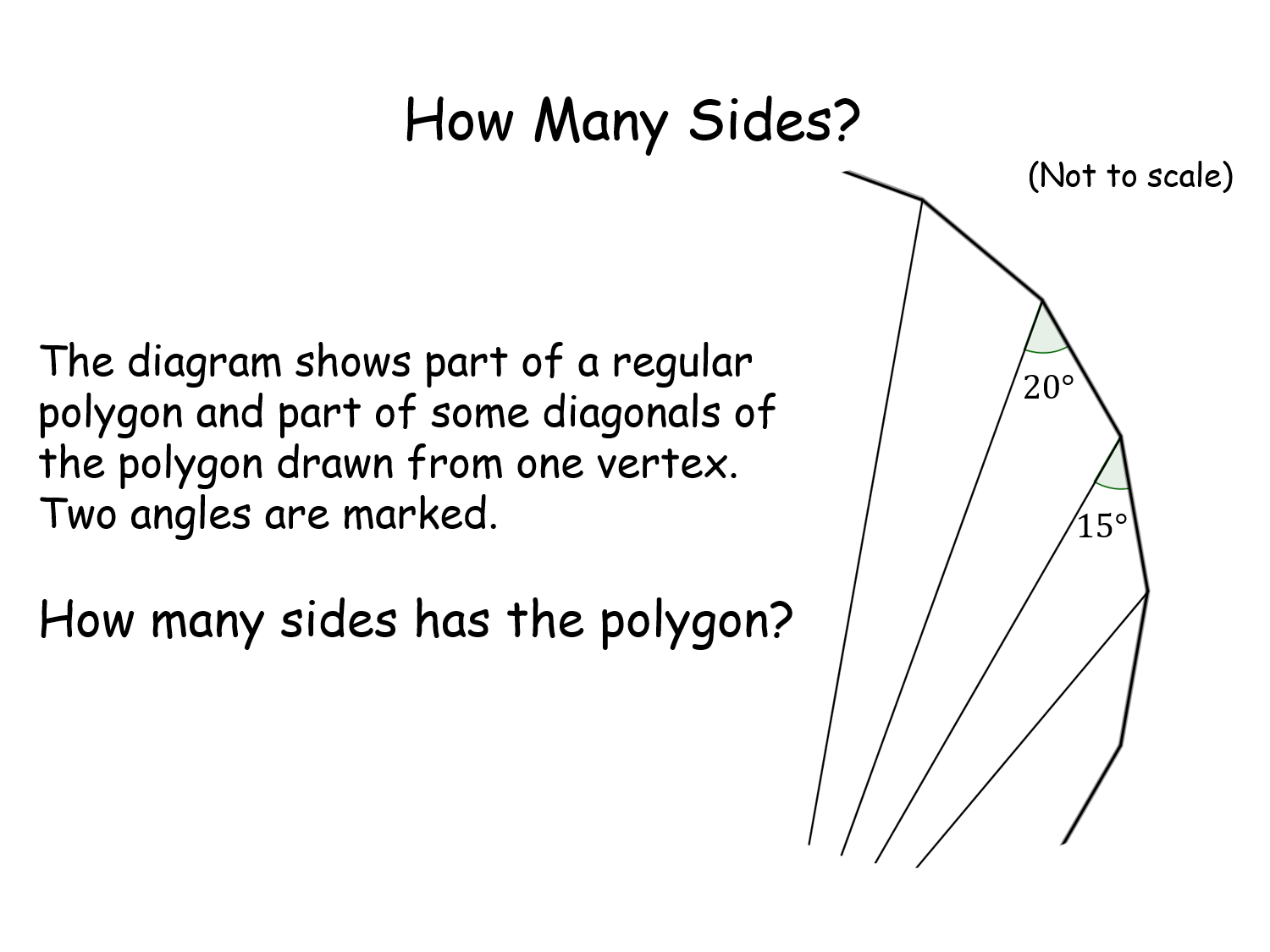
How Many Sides? |
On the face of it this looks like a very tricky problem but in fact it is quite straightforward, only requiring knowledge of external angles and the sum of angles in a triangle! Teacher can easily infer the answer and there is an interesting result at the end.How Many Sides? |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 48 |
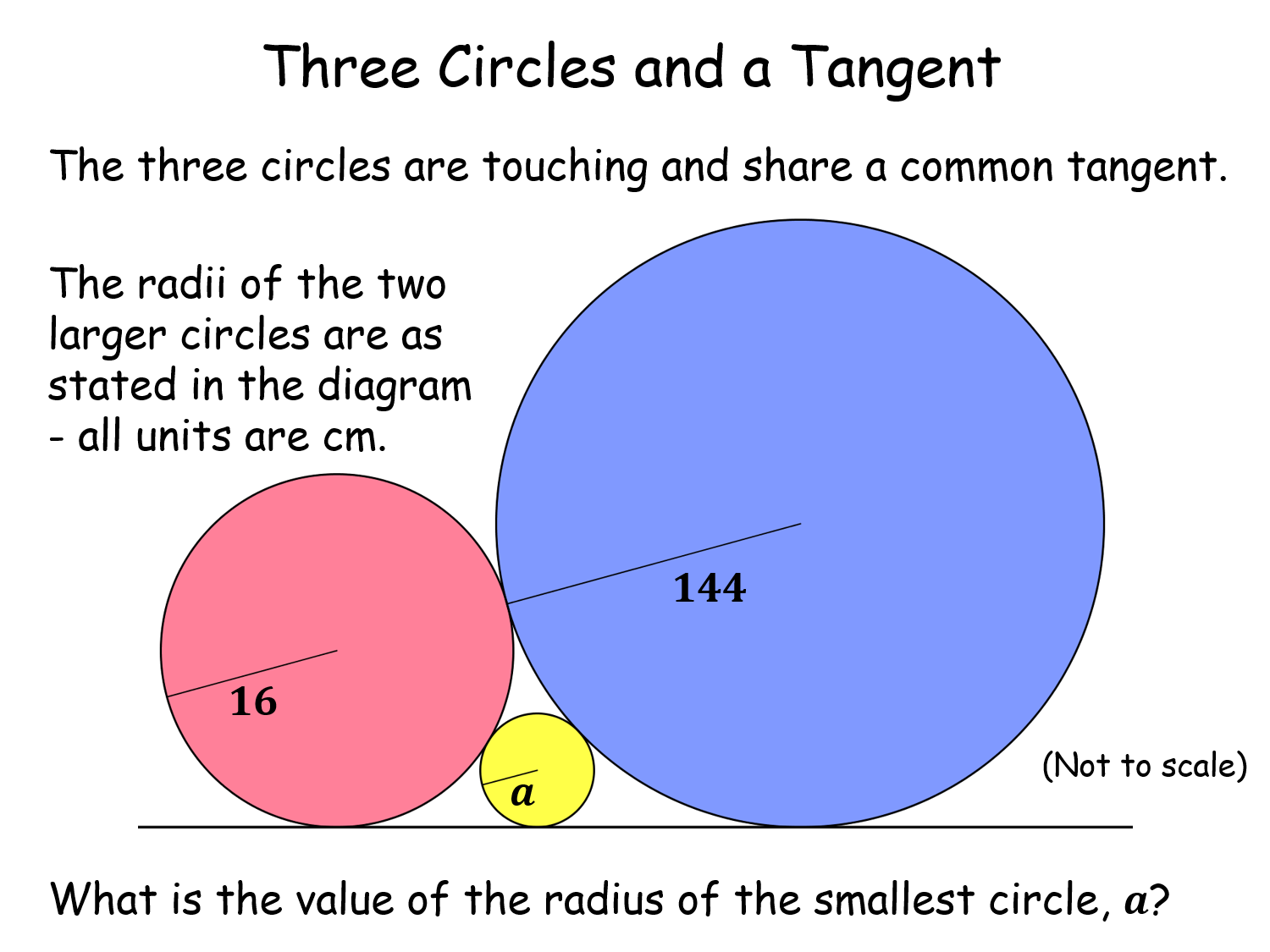
Three Circles and a Tangent |
Pupils seem to be fazed when they first look at this problem, so it's worth doing. It only requires Pythagoras' Theorem (like most Sangaku problems). There is a neat answer to the general case.Three Circles and a Tangent |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 49 |
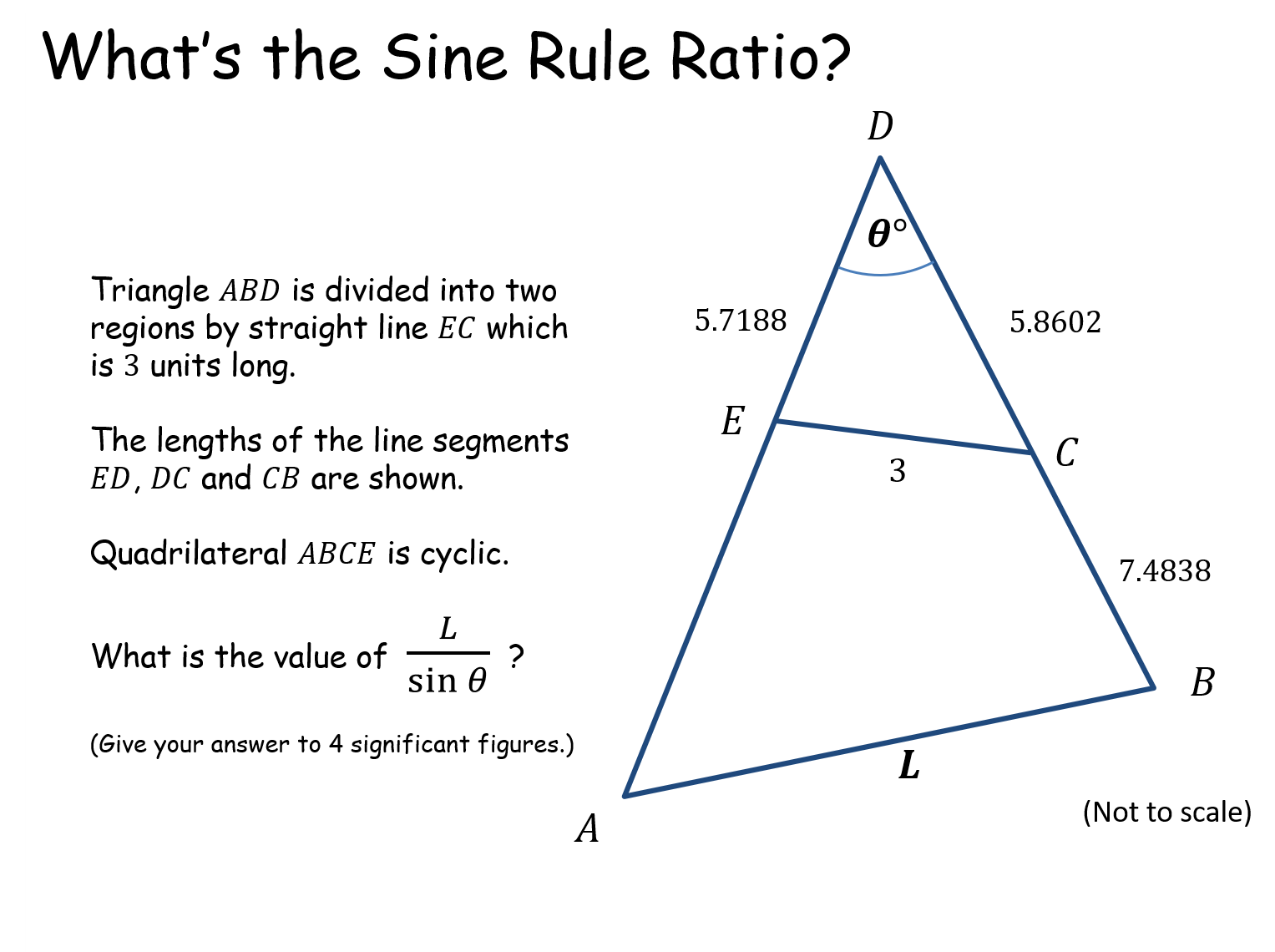
What's the Sine Rule Ratio? |
Pupils are asked to use their knowledge of sine rule, cosine rule and even a circle theorem or two to determine angles and lengths in a triangle.What's the Sine Rule Ratio? |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 50 |
Misprints Do Hapen |
Two proof-readers find errors in the same manuscript - but not all the same ones. How many are likely to have been missed by both? This problem seems intractable at first but is quite straightforward if you keep a clear head. The pupils should be challenged to create a new worksheet with the same answer, 2.Misprints Do Hapen |
H
Year 1 - Statistics
x_S_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 51 |
Equal Tangents |
This is a mixture of loci and coordinate geometry. It demonstrates a pleasing result that many teachers do not know about and its solution is delightfully simple and totally accessible, requiring no more than Pythagoras and a circle theorem.Equal Tangents |
F
Year 1 - Pure
x_R_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 52 |
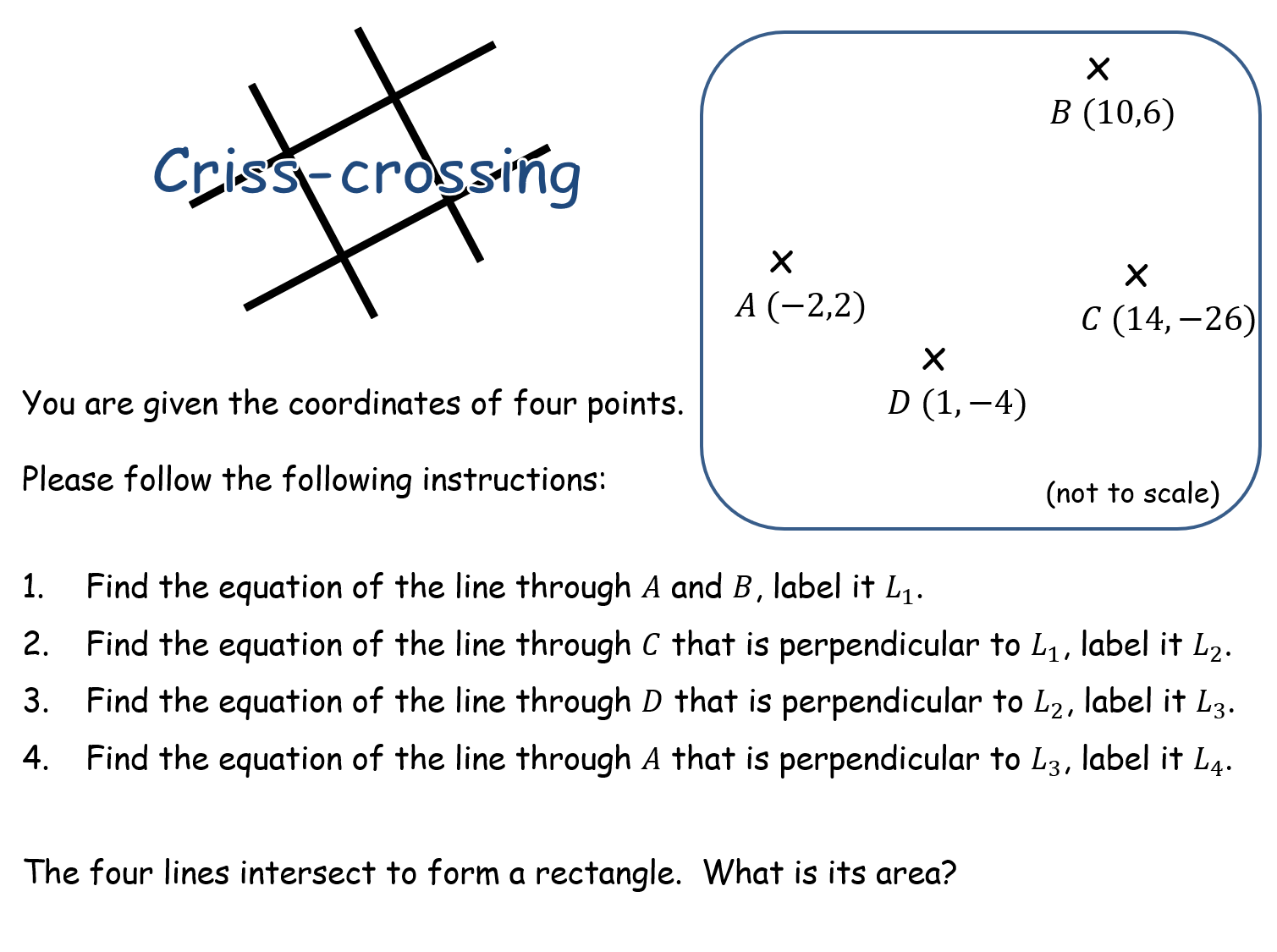
Criss-crossing |
An activity that hopefully tests their knowledge on everything they might need to know about straight lines: y=mx+c, gradient of perpendicular, intersection and simultaneous equations, distance between two points and calculating the midpoint of two points.Criss-crossing |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 53 |
Determine the Diagonals |
An activity that combines problem solving with the cosine rule. One of the diagonals is obvious, the other less so. Teacher can get the answer by simply adding two lengths, the pupils will need to work it out. All the quadrilaterals exhibit a special case of Ptolemy's theorem, which can be introduced for enrichment.Determine the Diagonals |
E_
Year 11
x_E_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 54 |
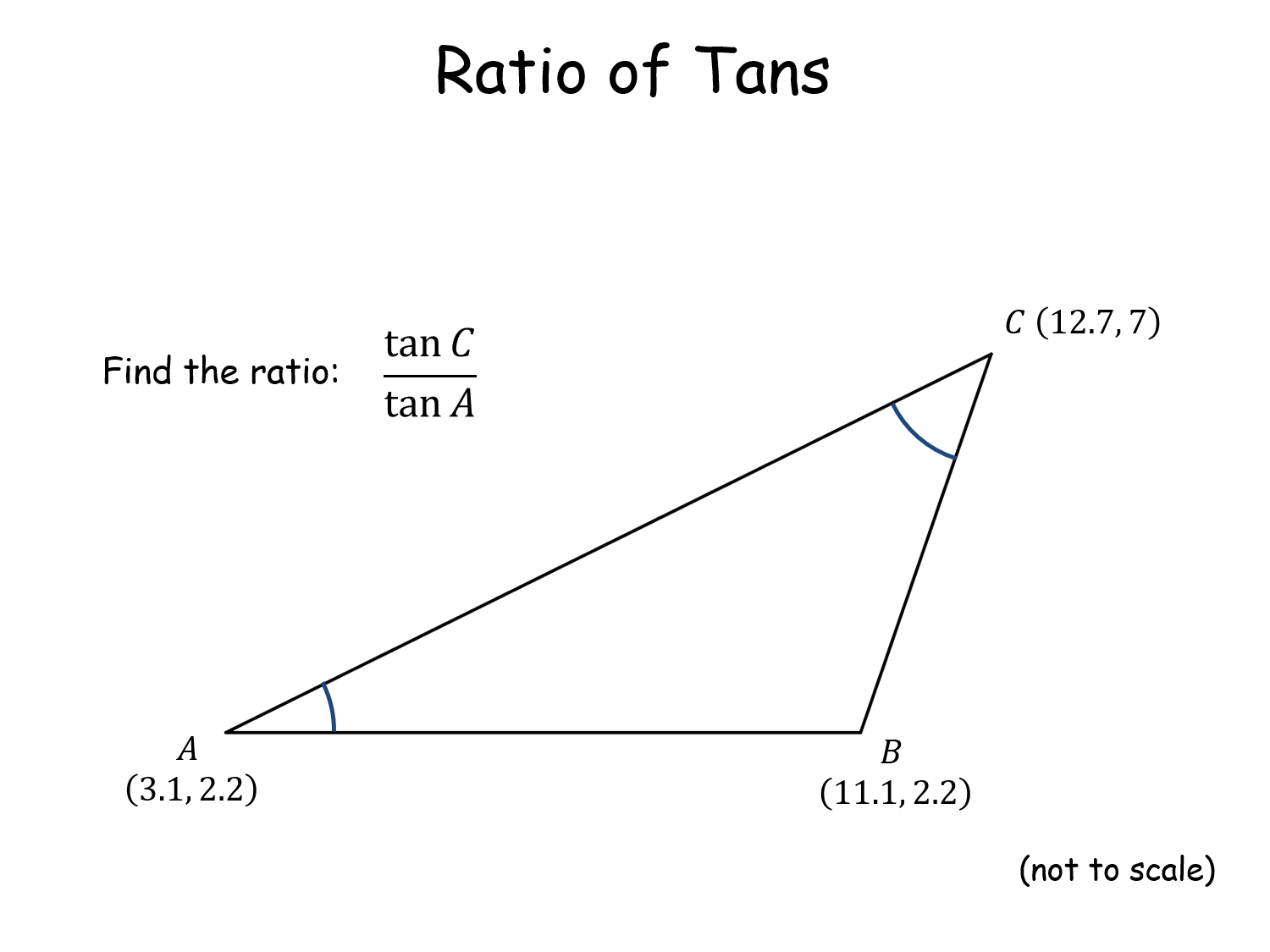
Ratio of Tans |
Given seemingly random triangles the pupils need to calculate the ratio of the tangents of two named angles. For every triangle the answer is 2. They need to understand a little coordinate geometry, how to get sine from tangent, use the sine rule. Proof of the answer requires a circle theorem and some geometry.Ratio of Tans |
J
Year 2 - Pure
x_T_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 55 |
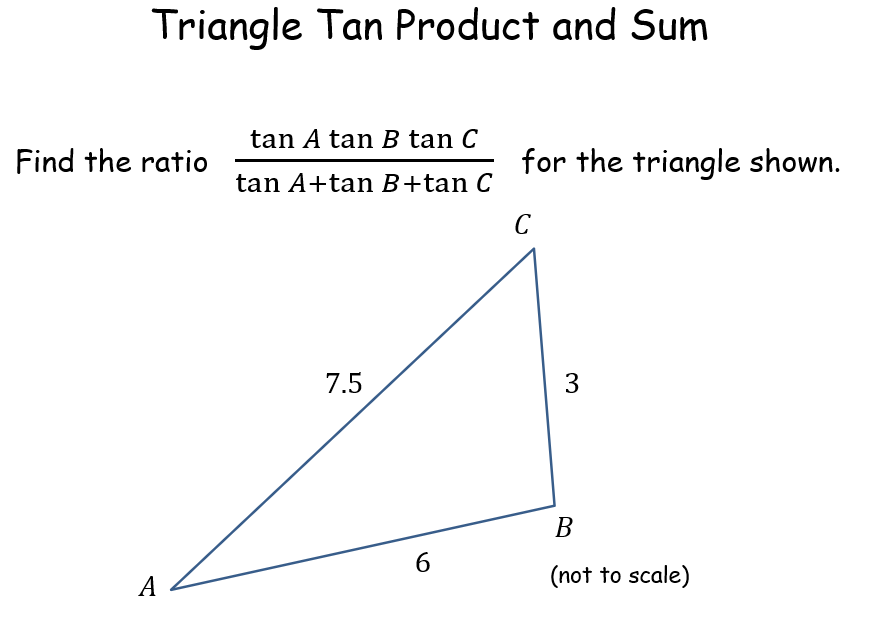
Triangle Tan Product and Sum |
Pupils are given triangles (whose sides follow a pattern but this is just a red herring) and they must determine the product of the tan of each angle and the sum of the tan of each angle. Why are they equal? Were the triangles special? They must investigate the general case and prove this identity that doesn't seem very well known.Triangle Tan Product and Sum |
J
Year 2 - Pure
x_T_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 56 |
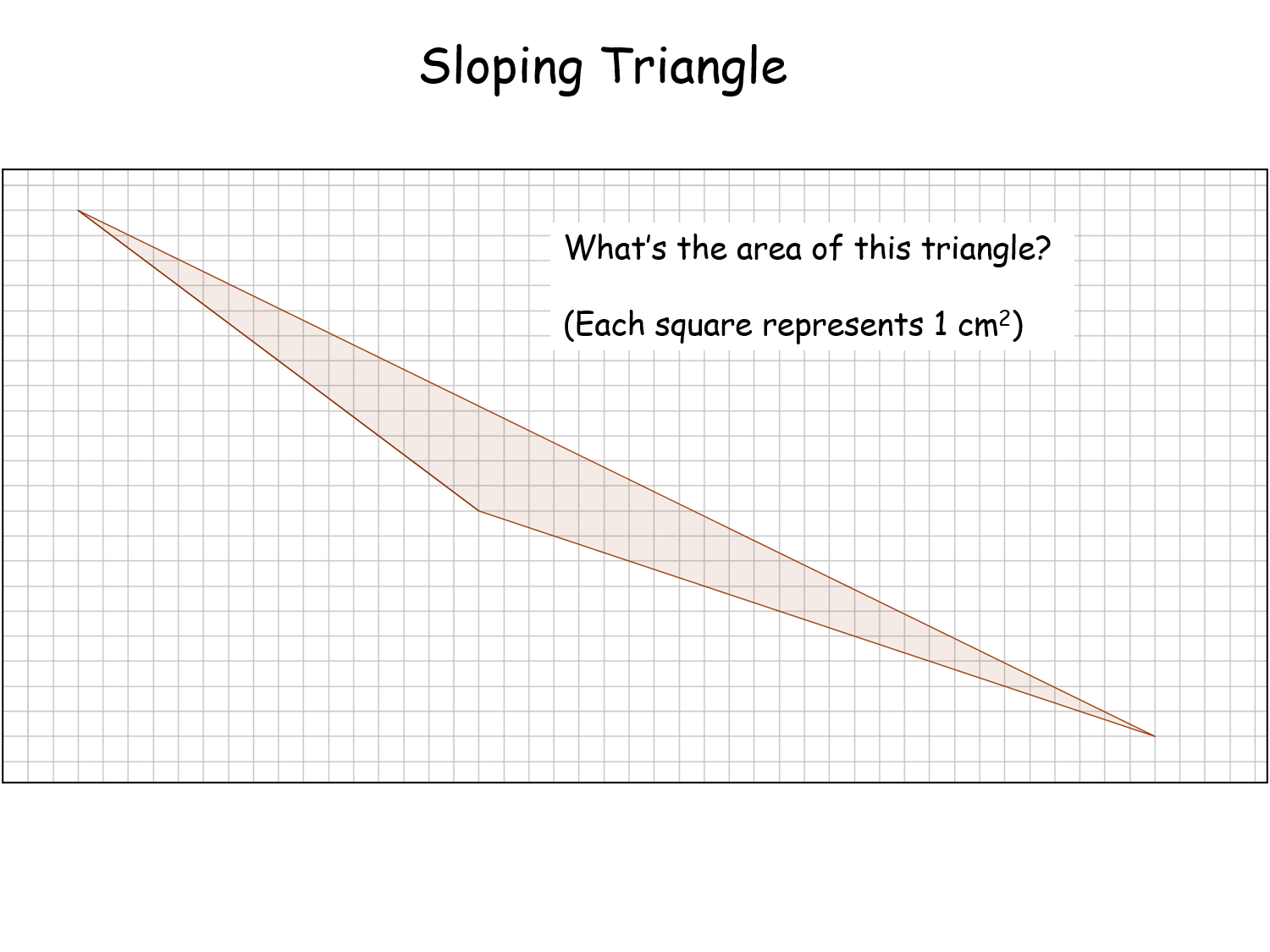
Sloping Triangle |
Pupils are given a scalene triangle on a grid and they have to work out its area. Counting squares is awkward and so they need to add triangles, rectangles or trapeziums and determine the area by area subtraction. But there is a neat way to work out the area with just one area calculation. Can they find it?Sloping Triangle |
C_
Year 9
x_C_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 57 |
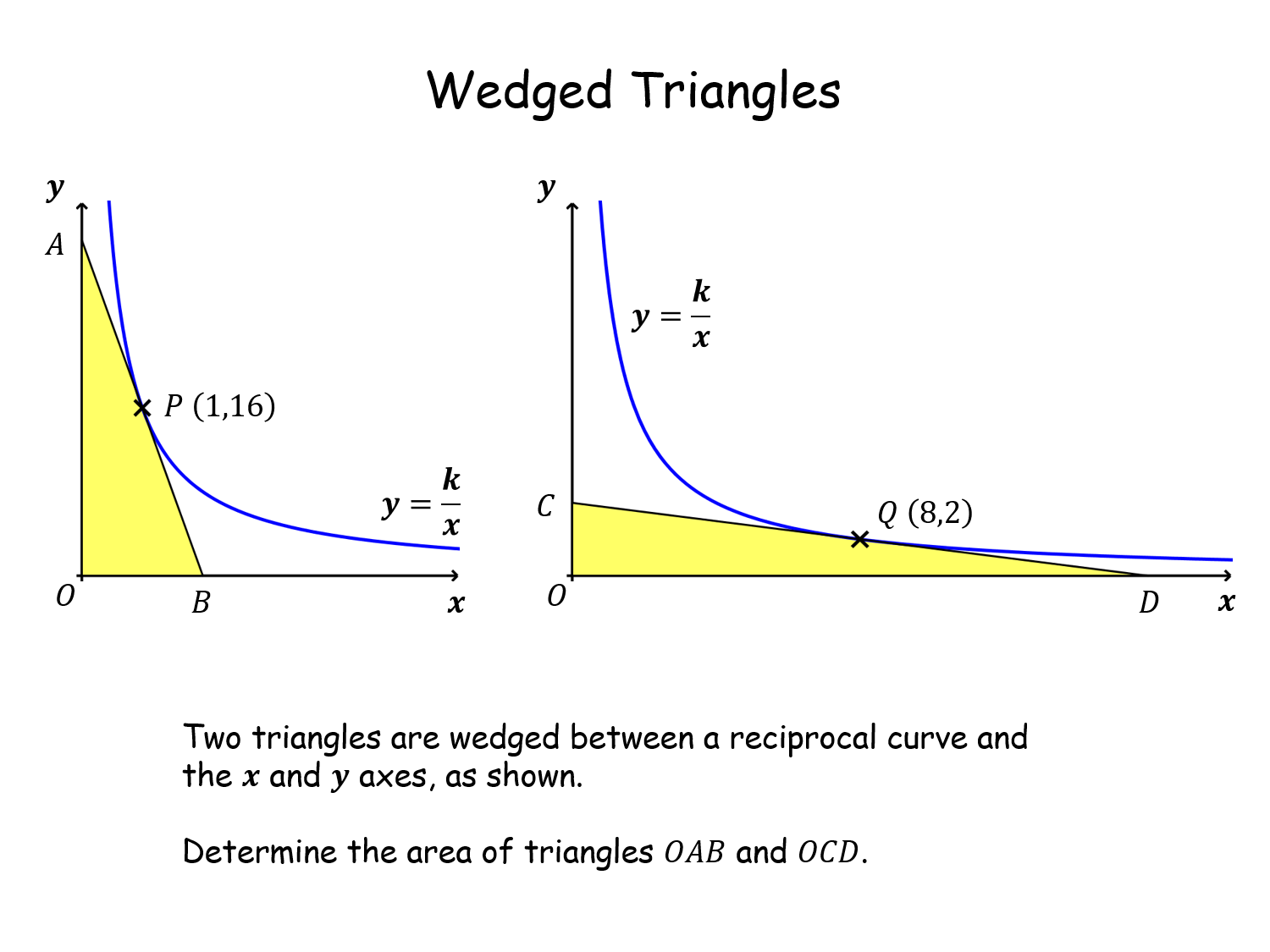
Wedged Triangles |
Pupils are given two triangles that are wedged between a reciprocal curve and the x and y axes. Their job is to work out their areas (which are equal to each other and easy for the teacher to ascertain). Can they prove why they are equal? Involves diffferentiation and equations of straight lines.Wedged Triangles |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Adobe PDF) (Adobe PDF) |
|
|
| 58 |
Straight Line and Circle |
A very simple (but illuminating) task where pupils have to find the equation of a straight line that is tangential to an unknown circle centred on the origin. They are given the coordinates of a single point on the line so it ties a few concepts together. The coordinates appear in the answer, making it easy for teacher!Straight Line and Circle |
E_
Year 11
x_E_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 59 |
What's f(500)? |
Problem solving activity taken from the UK Mathematics Trust Senior Mathematics Challenge 2015. I have simply created additional starting points that all end up with the same answer.What's f(500)? |
F
Year 1 - Pure
x_R_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 60 |
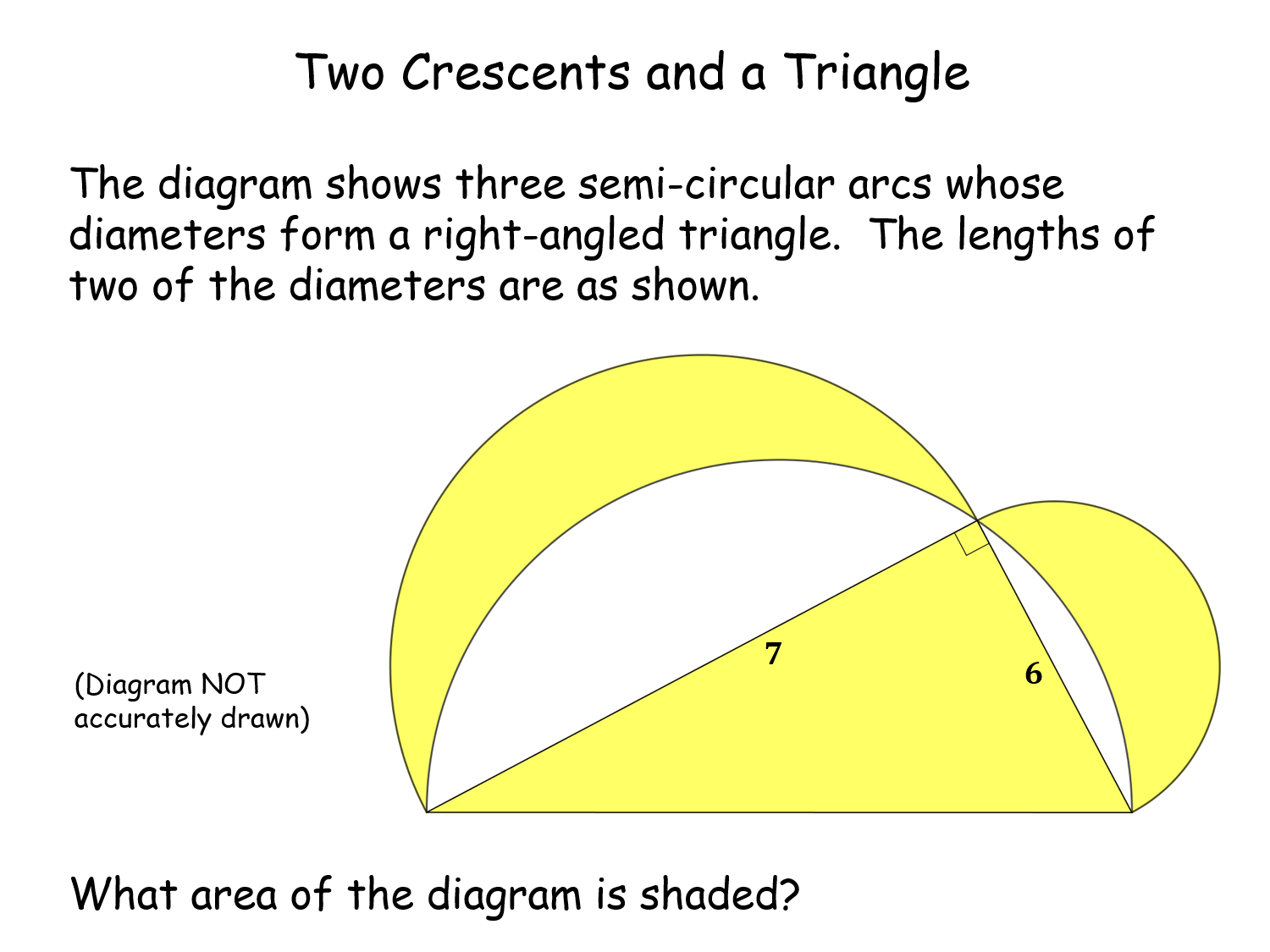
Two Crescents and a Triangle |
A problem solving activity using area of the circle and triangle and bringing them together using Pythagoras. All answers are different but very easy for the teacher to know the answer from numbers on the worksheet. Ends with the realisation that Pythagoras does not have to have "squares".Two Crescents and a Triangle |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 61 |
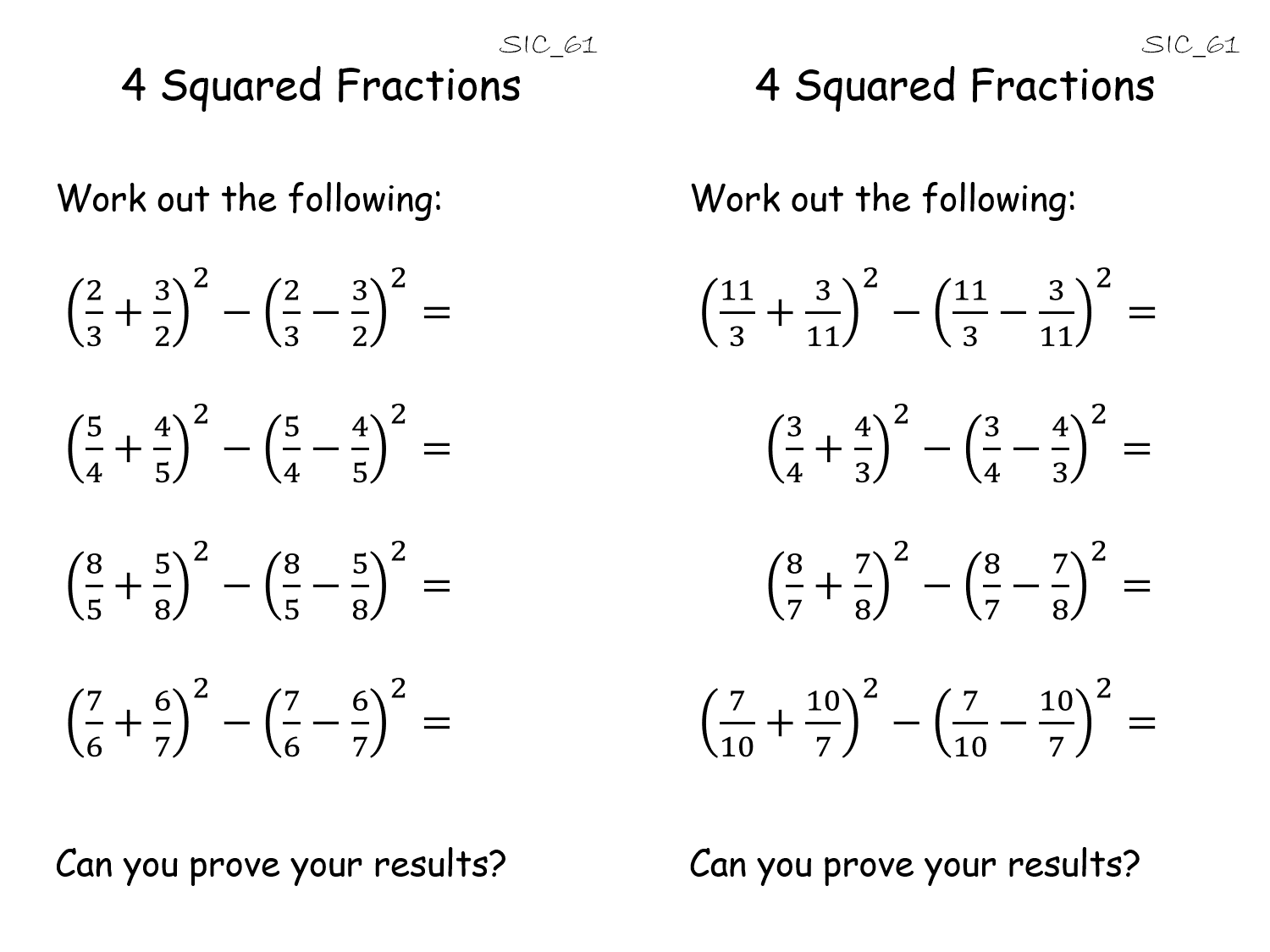
4 Squared Fractions |
Practice with fractions. An activity that gives an unexpected result with fraction addition/subtraction/squaring. Because of the pattern of numbers used the answer is always 4. This is a surprising result which the pupils then need to prove.4 Squared Fractions |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 62 |
Three Triangles and a Square |
Practice with surds and a little problem solving. Pupils have to find missing lengths in triangles to eventually obtain the side of the square (which is the same for all worksheets).Three Triangles and a Square |
D_
Year 10
x_D_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 63 |
An interesting pair of Simultaneous Equations |
Practice with non-linear simultaneous equations with disguised circles. Two circles intersect a given line at the same points. Ends with an unusual result - subtracting the circle equations gives the equation of the common chord (which is the given straight line).An interesting pair of Simultaneous Equations |
F
Year 1 - Pure
x_R_x |
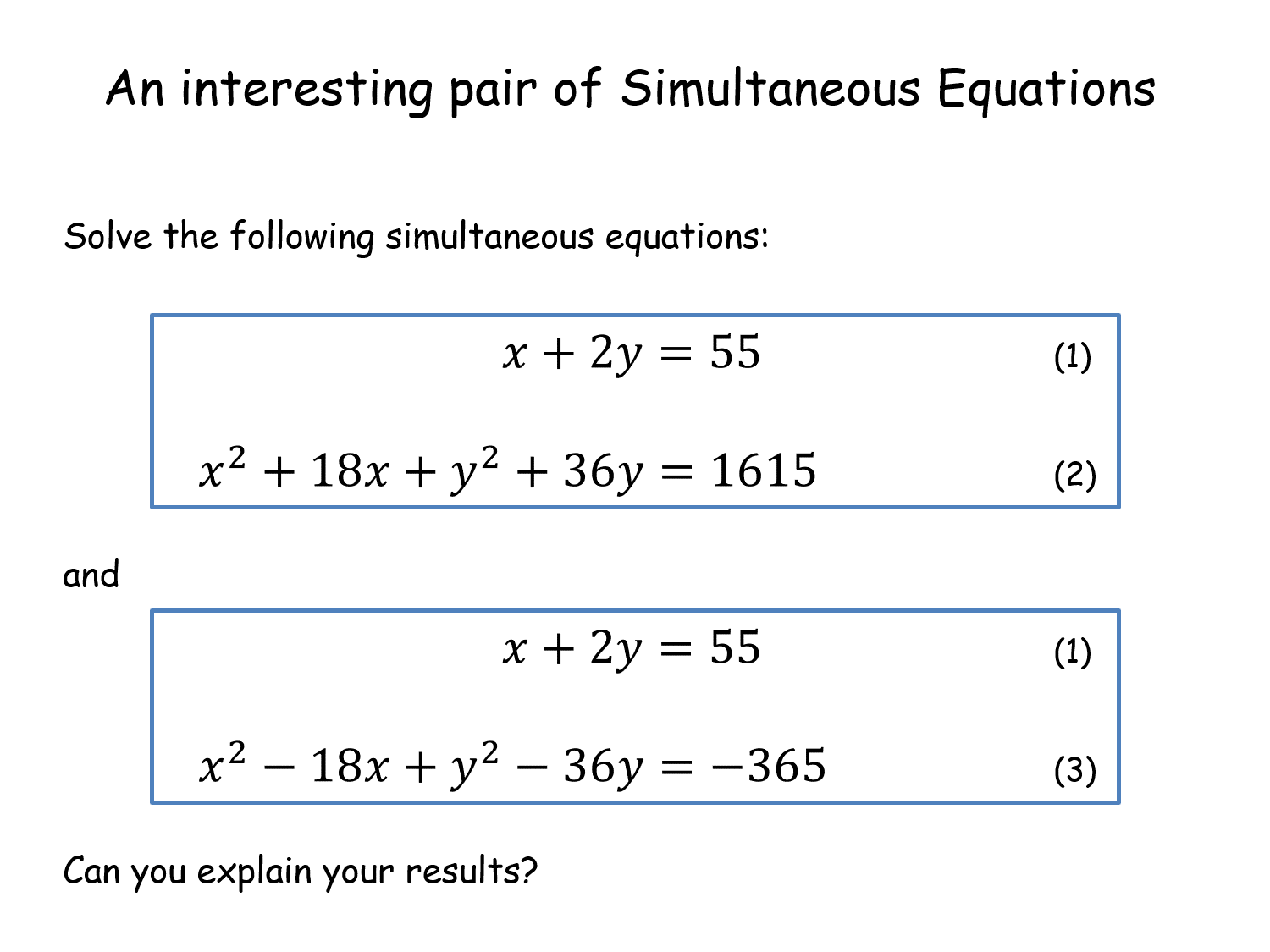
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 64 |
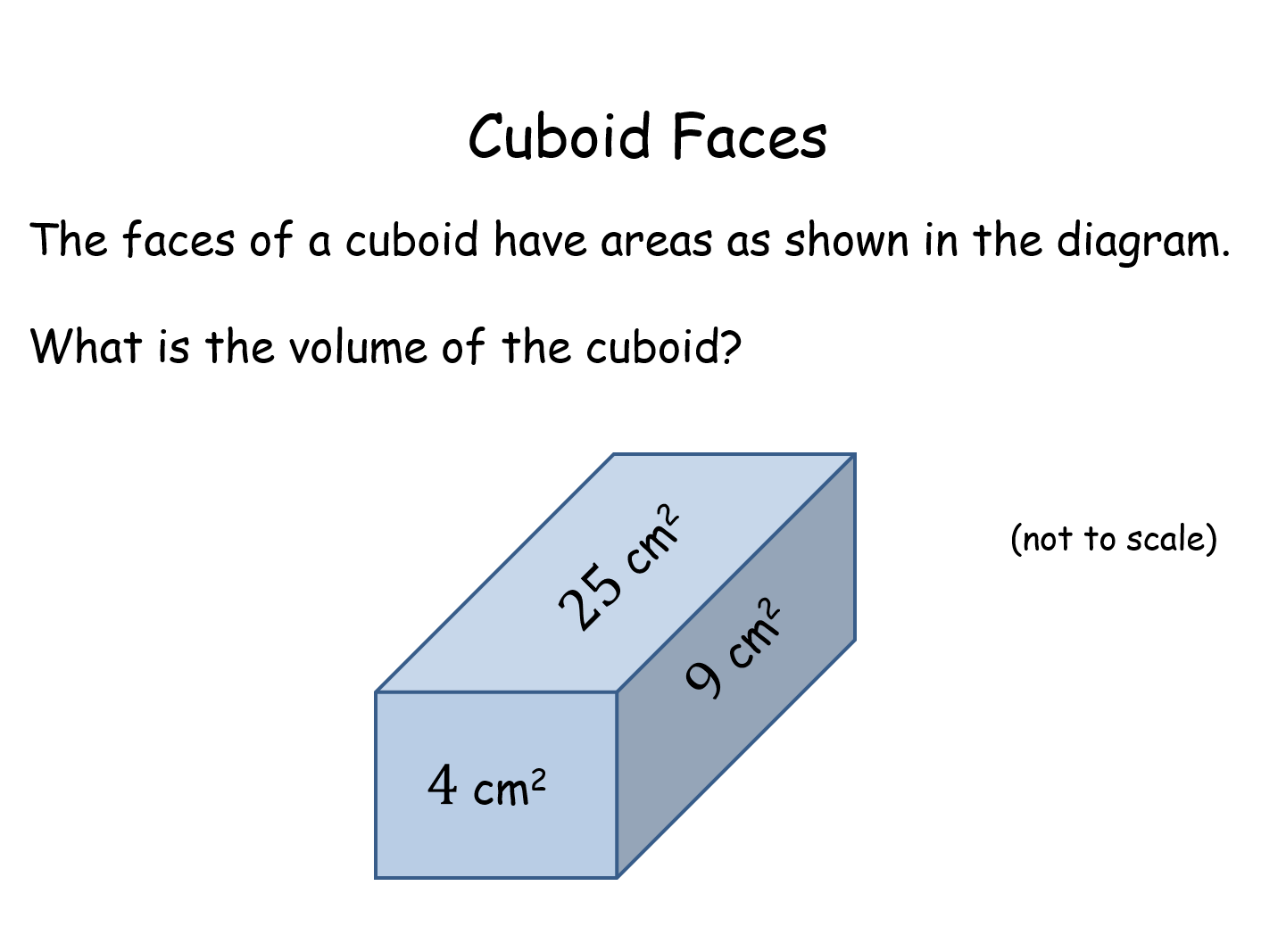
Cuboid Faces |
Problem solving activity taken from nRich. Pupils need to determine the volume of a cuboid given only the areas of it faces. There is a nice alternative solution twist at the end.Cuboid Faces |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 65 |
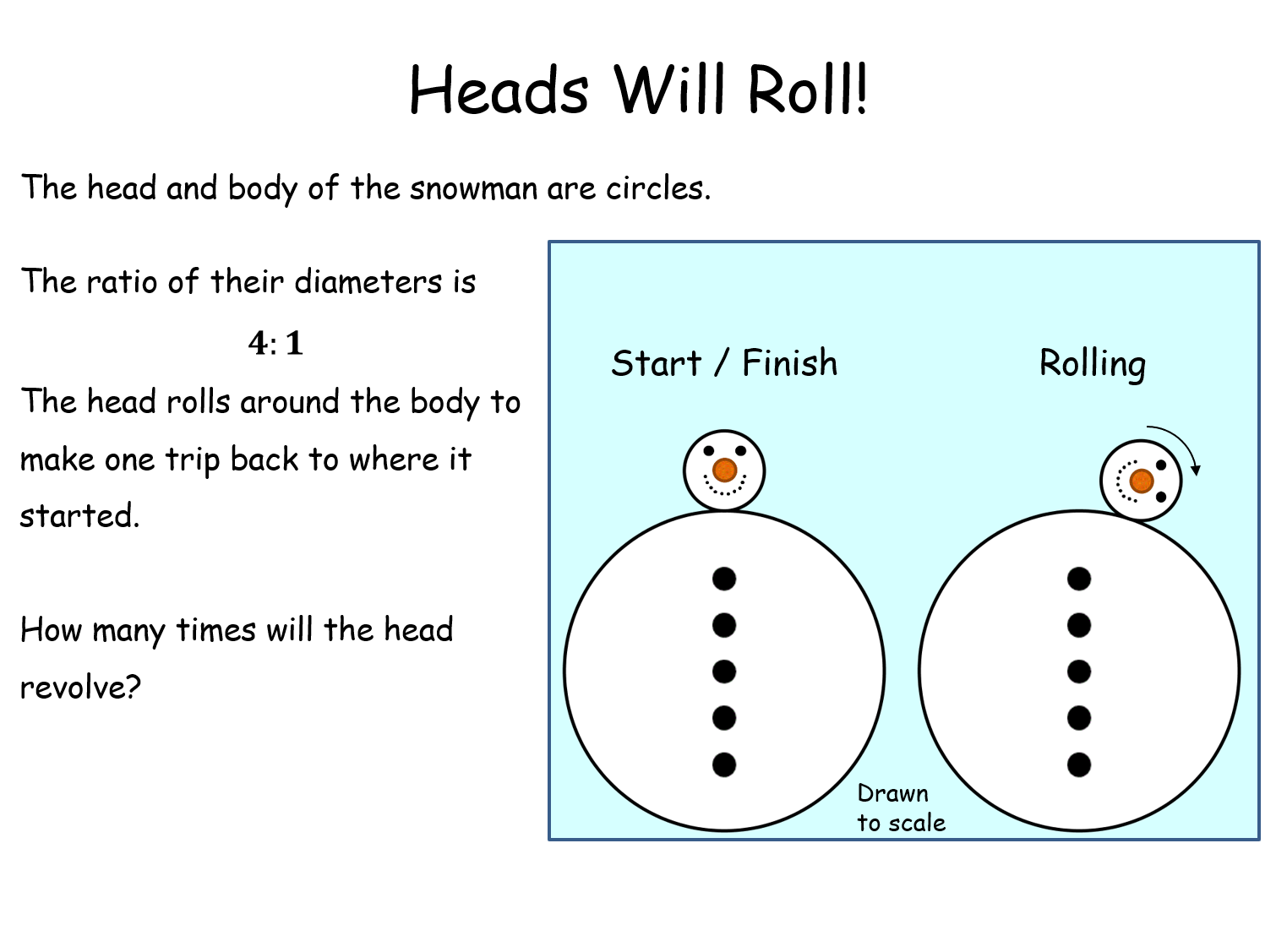
Heads will roll! |
A winter-themed version of the classic rolling circles problem that many are probably unaware of.Heads will roll! |
C_
Year 9
x_C_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 66 |
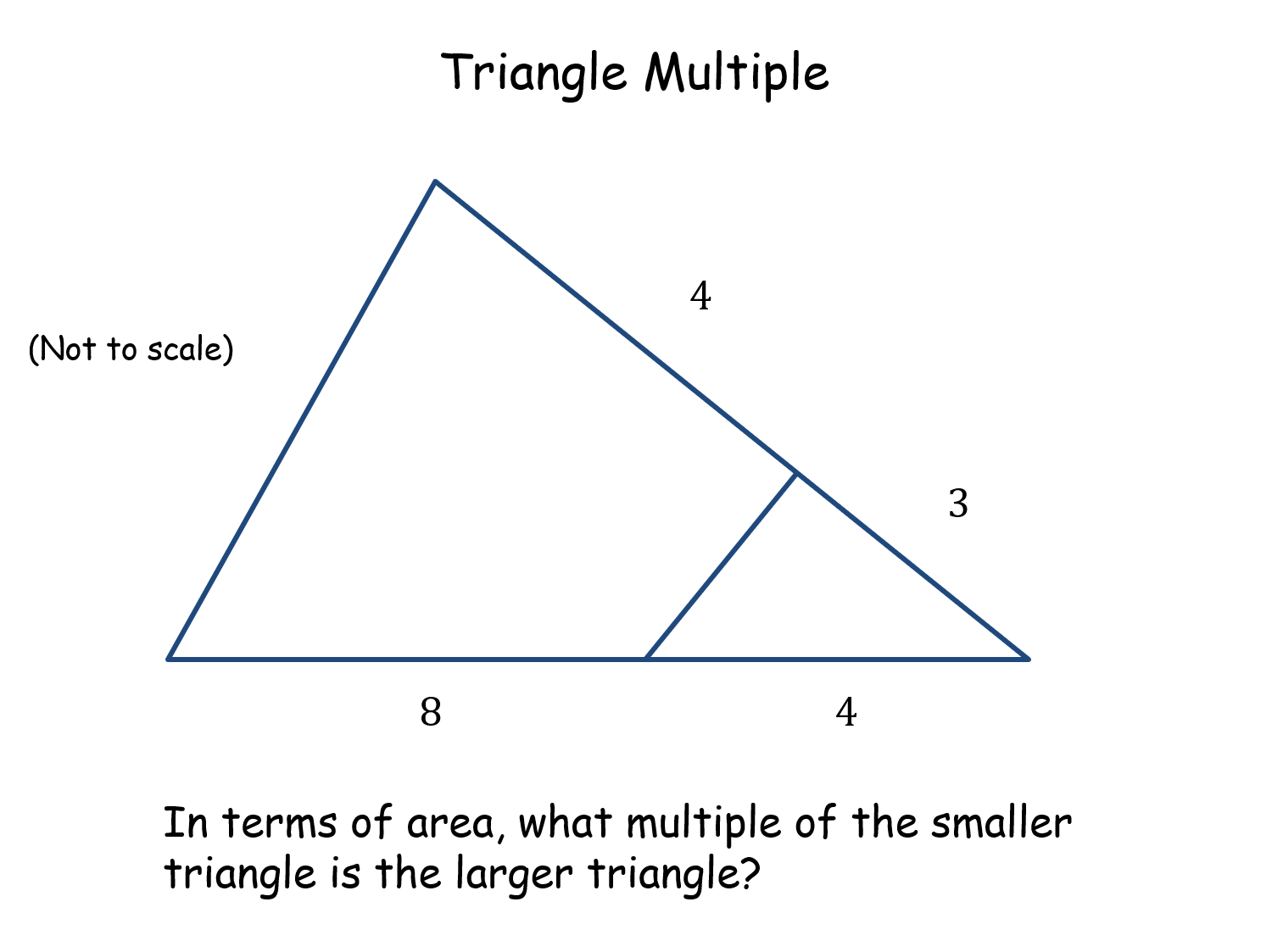
Triangle Multiple |
One of those problems where it looks like that you don't have enough information. A little thought shows that it only requires knowledge of the area of triangles. There is a nice twist at the end where changing one of the values does not affect the answer. Many thanks to ATM's "Forty Harder Problems for the Classroom".Triangle Multiple |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 67 |
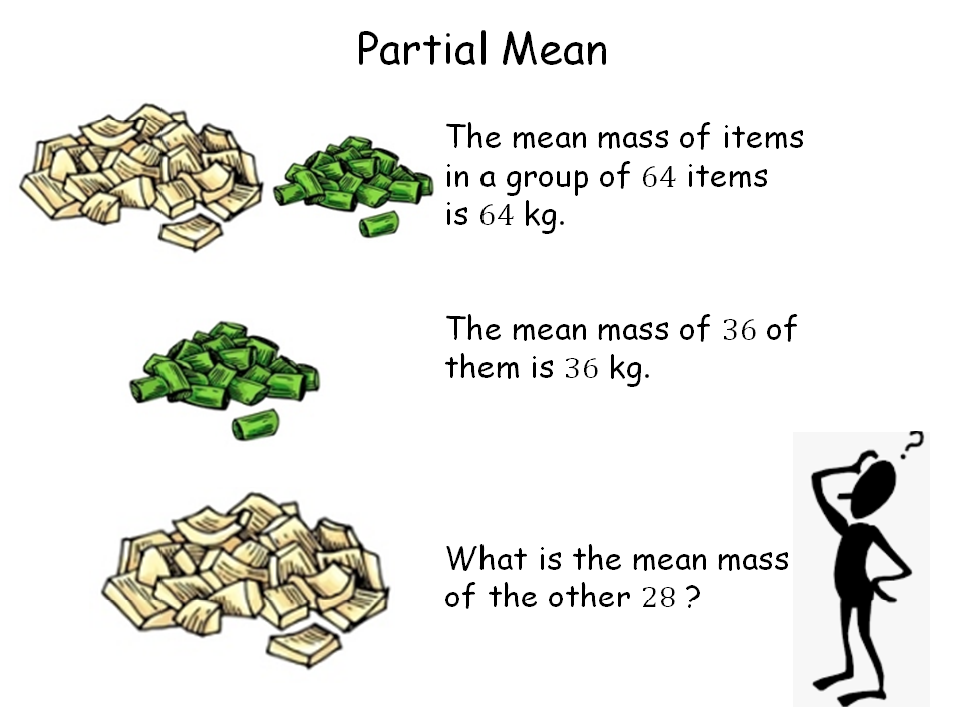
Partial Mean |
A problem to see if the pupils really do understand how to calculate means of numbers. Another rich resource taken from nRich. Some big numbers are involved but you can challenge them to solve it without a calculator (easy if you know about the difference of two squares).Partial Mean |
C_
Year 9
x_C_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 68 |
Train Length |
A classic speed-distance-time problem which exemplifies reading the question properly and is good practice at problem solving. The equation is easy to solve, but only if you form it correctly. The answer is half the train tunnel length - can they work out why this is the case? A simple, accessible proof is all that is required.Train Length |
G
Year 1 - Mechanics
x_S_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 69 |
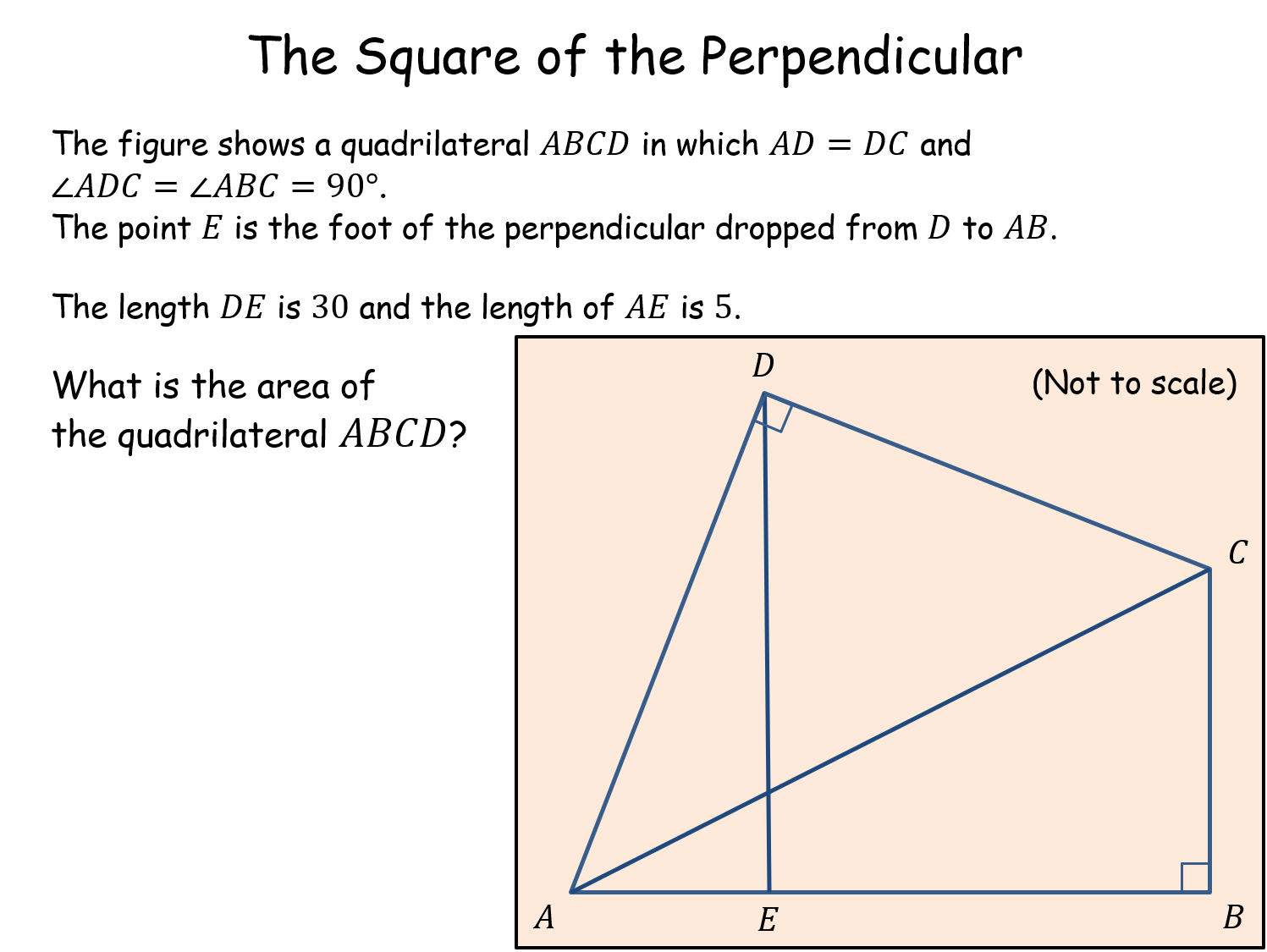
The Square of the Perpendicular |
A problem solving resource which utilises Pythagoras and circle theorems (but not obviously) to work out the area of a specially constructed quadrilateral. Pupils are invited to look at the general case to explain their findings. The idea for this resource came from a UKMT Senior Kangaroo paper.The Square of the Perpendicular |
J
Year 2 - Pure
x_T_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 70 |
What's f(20nn)? |
An example of where calculators can let you down! Pupils have to simply evaluate a given function but they won't achieve the required level of accuracy by calculation. Resorting to algebra (with a link to rationalising surds) gives the correct answer.What's f(20nn)? |
E_
Year 11
x_E_x |
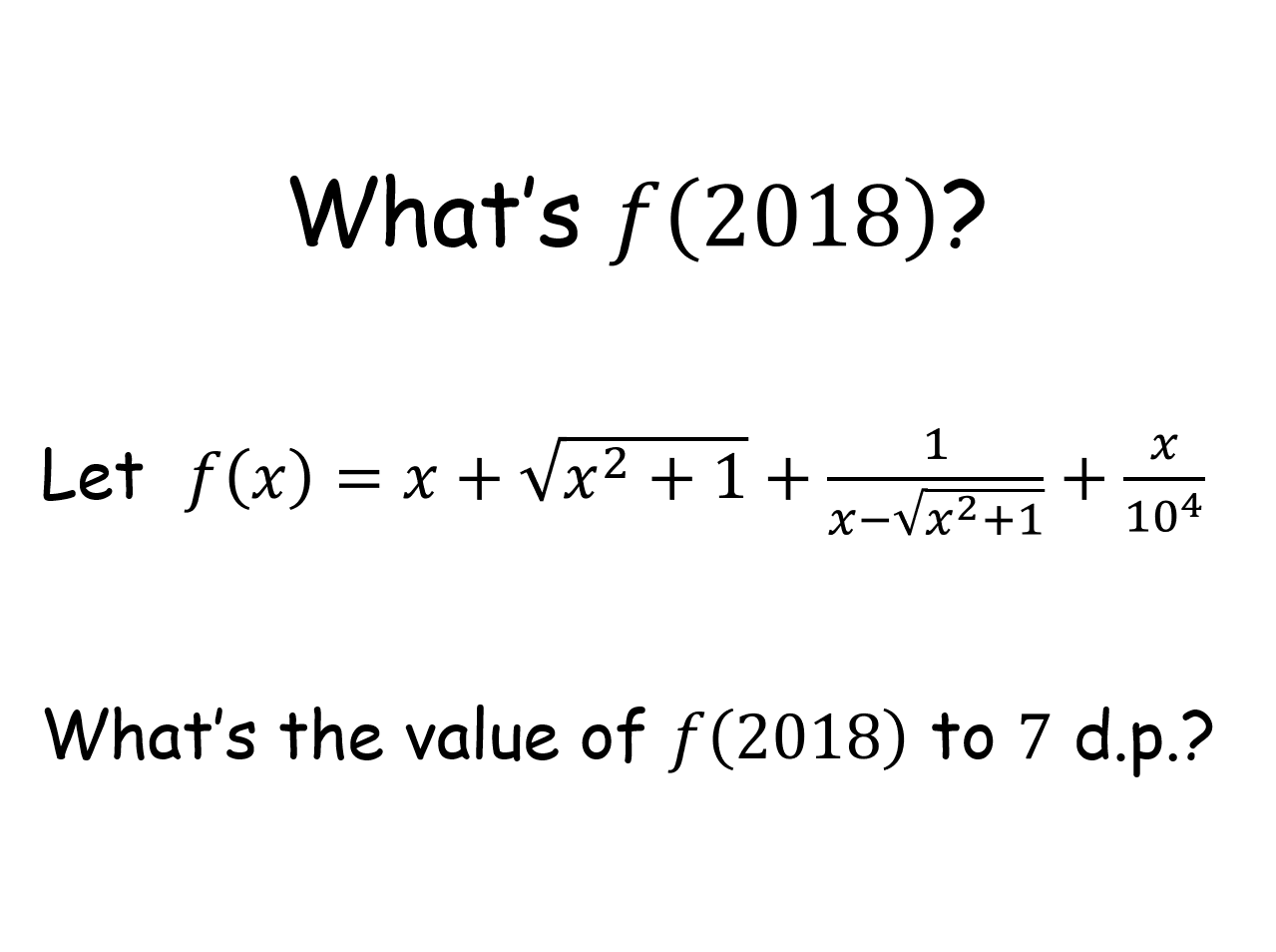
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 71 |
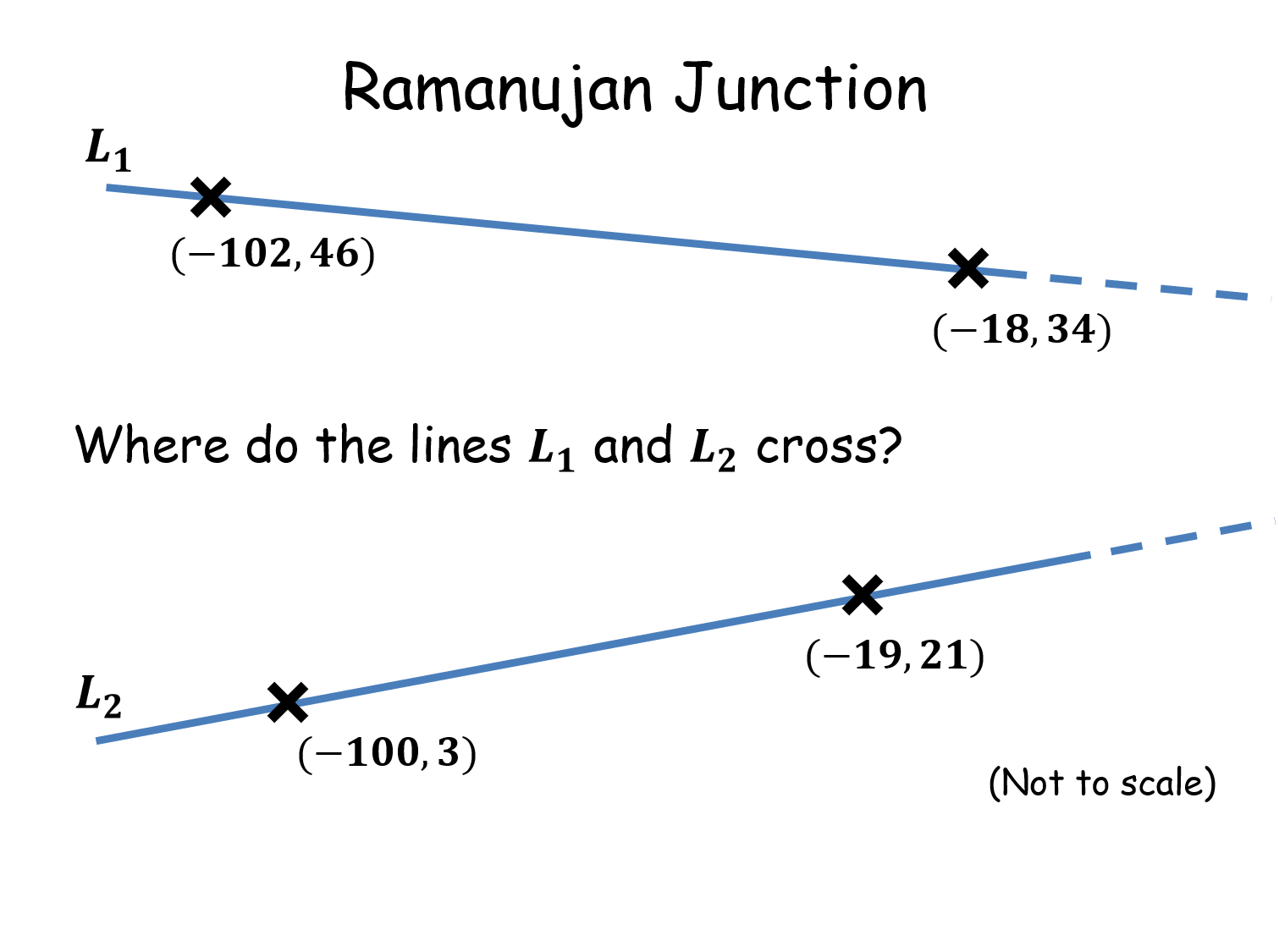
Ramanujan Junction |
This activity tests pupils' knowledge of gradients, straight line graphs and simultaneous equations (and the link with crossing lines). The answer lies in the title, being (17,29). The lines on each worksheet are the same, only the coordinates differ.Ramanujan Junction |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 72 |
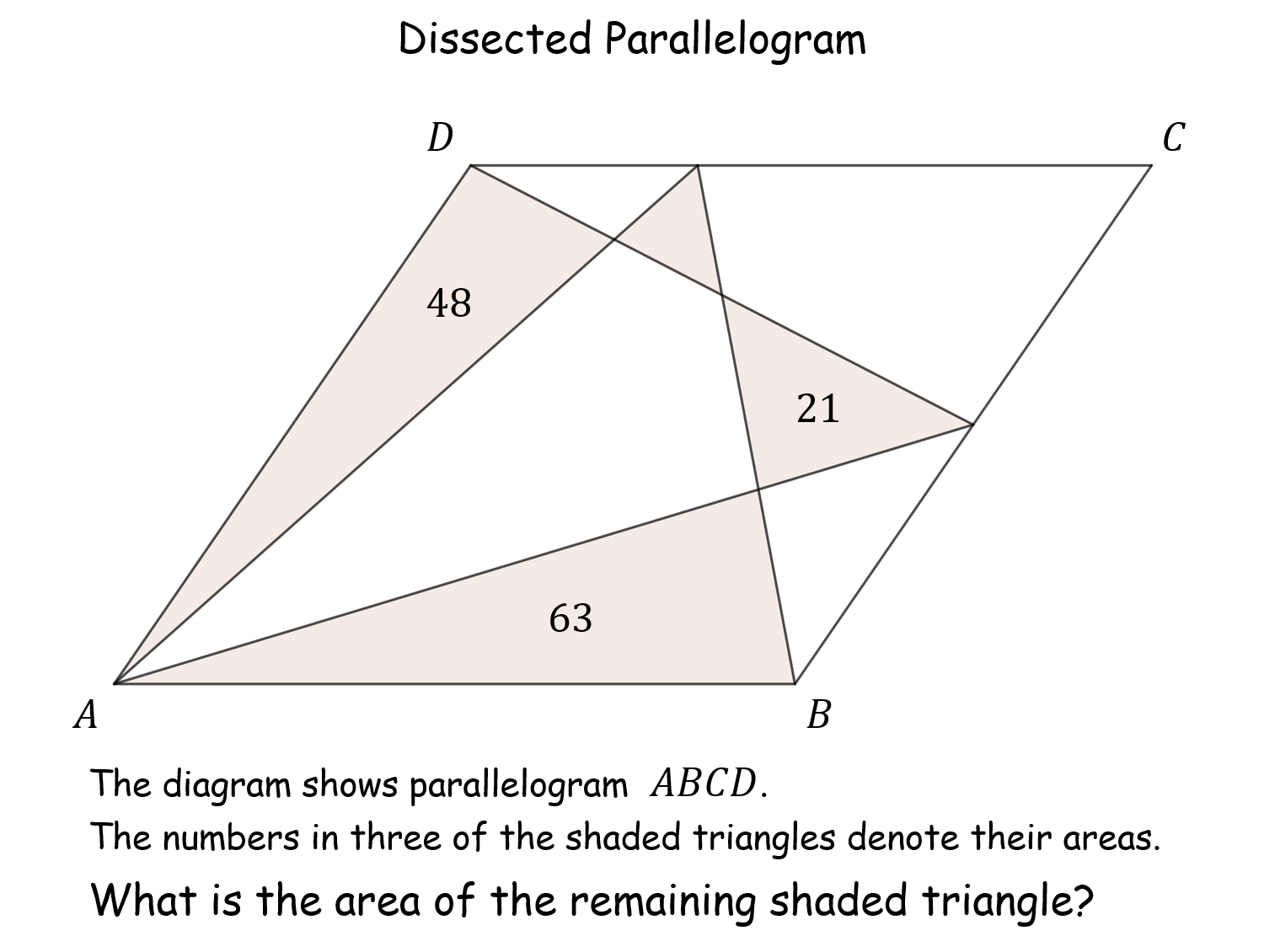
Dissected Parallelogram |
Most pupils will have no clue as to how to start this problem. Teacher will probably need to scaffold with the idea that shearing a shape does not change its area. So the parallelogram is mapped to a rectangle. The problem reduces to knowledge of areas of triangles.Dissected Parallelogram |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 73 |
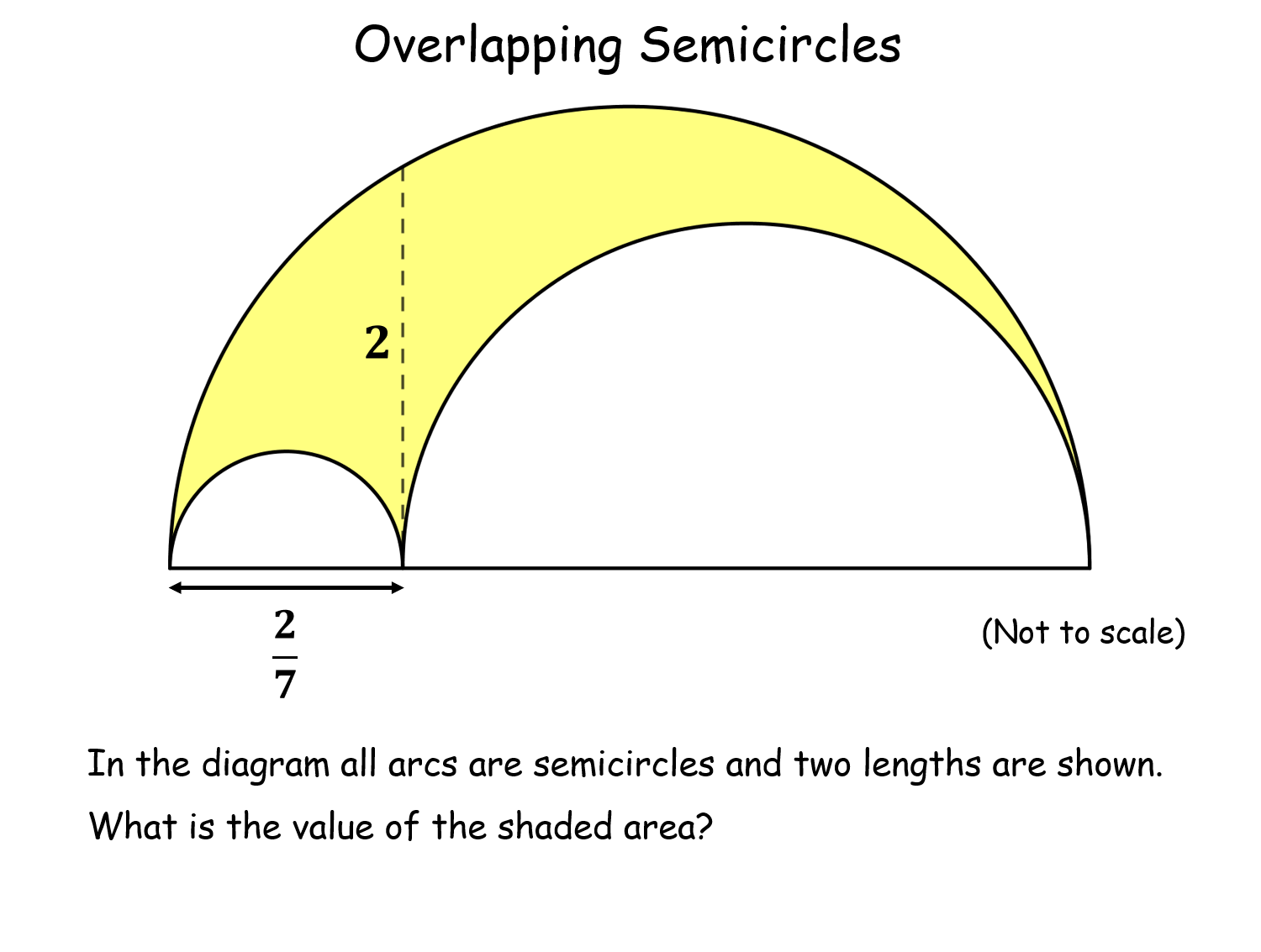
Overlapping Semicircles |
This activity brings together a circle theorem, Pythagoras and proof. Similarity can also be used and a neat way using the intersecting chords theorem is also shown. All answers are the same (pi) and the pupils are invited to prove it, reproducing their calcualtions with letters in place of numbers.Overlapping Semicircles |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 74 |
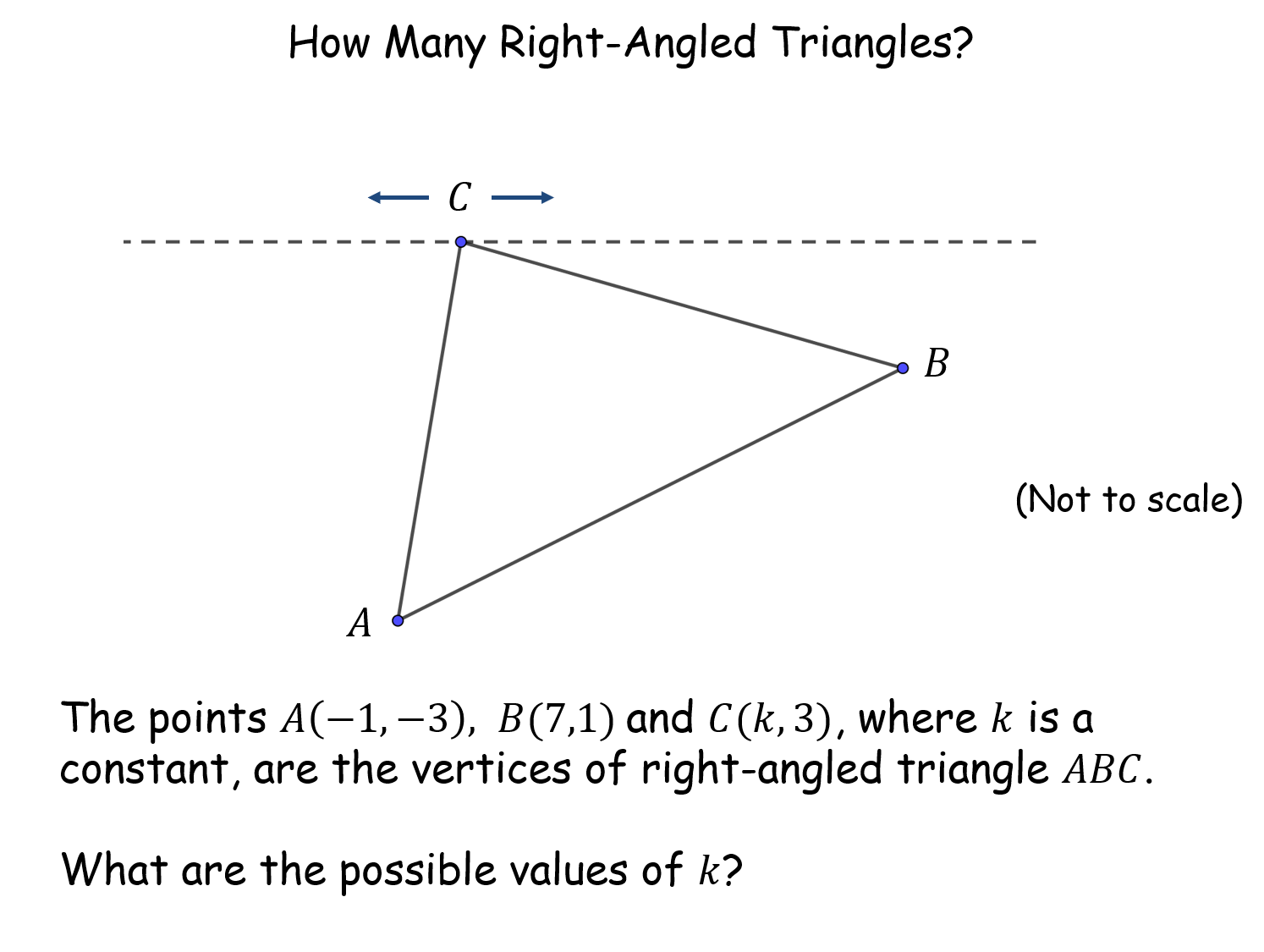
How Many Right-Angled Triangles? |
Most pupils will use Pythagoras to solve this problem. But it is instructive to use gradients of perpendicular lines to solve it also. The result surprises many (there are four such triangles) and a circle theorem explains why. An extension utilises the discriminant to find a unique solution.How Many Right-Angled Triangles? |
F
Year 1 - Pure
x_R_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 75 |
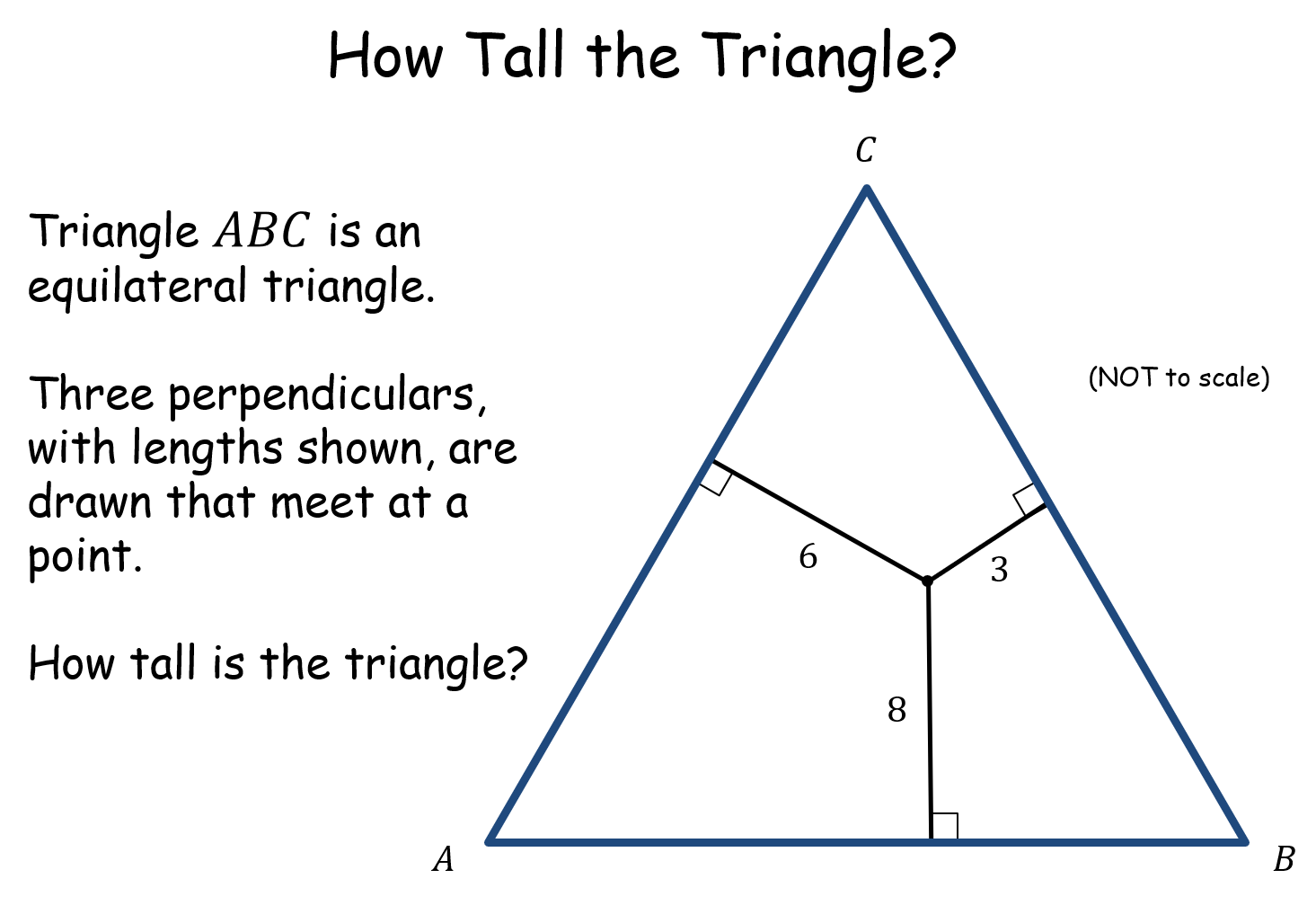
How Tall the Triangle? |
Most pupils will find this a bit tricky at first because they are unlikely to have seen anything like it before so it is a good problem solving activity. It utilises a really neat result so that Teacher only needs to sum the three lengths to arrive at the unique answer. The proof is not difficult.How Tall the Triangle? |
F
Year 1 - Pure
x_R_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 76 |
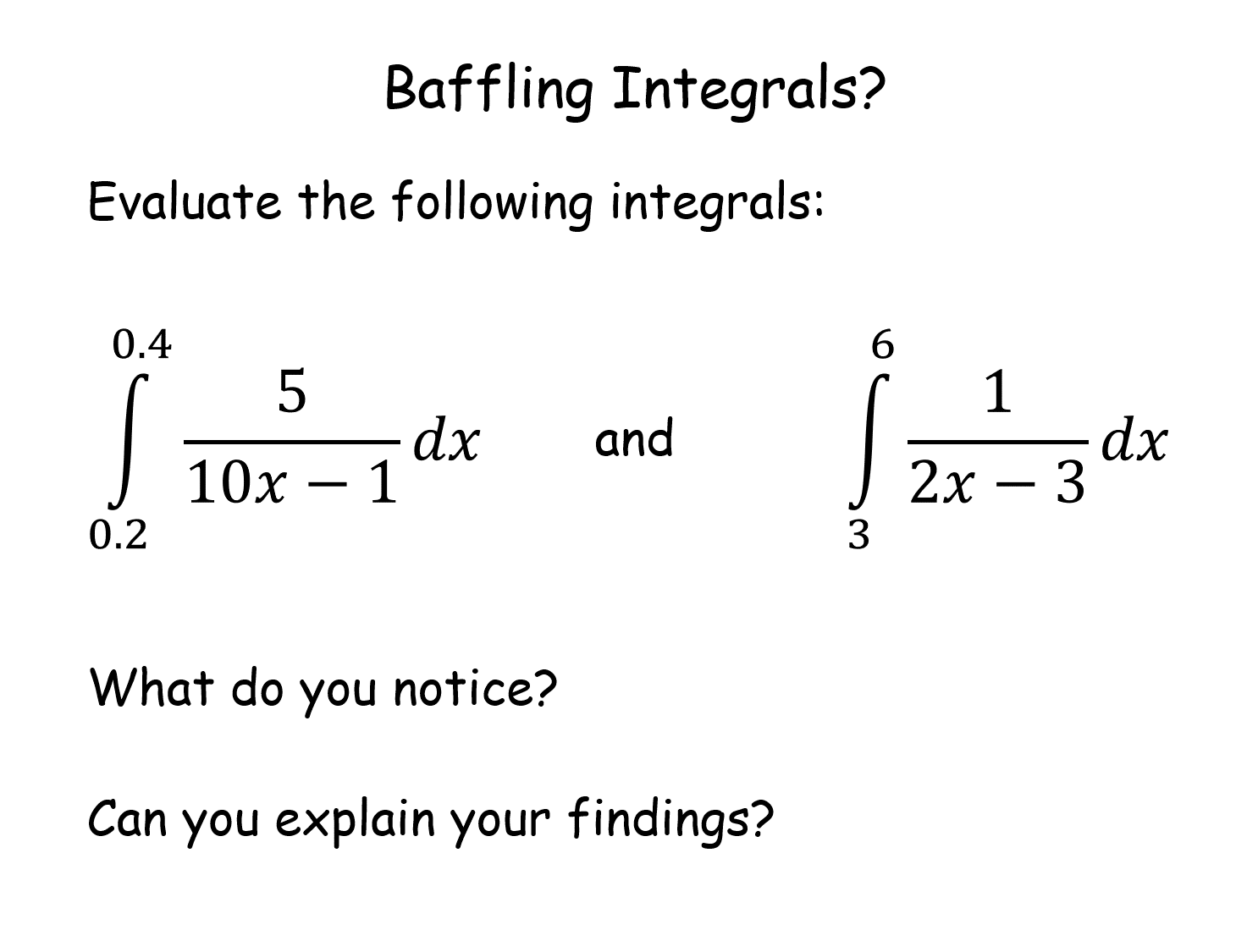
Baffling Integrals? |
Pupils are given two integrals to evaluate. They do not look related at first sight but they evaluate to the same value. In fact, the whole class get the same result and they are invited to investigate why. This activity links transformations and the affect (or not) on areas.Baffling Integrals? |
F
Year 1 - Pure
x_R_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 77 |
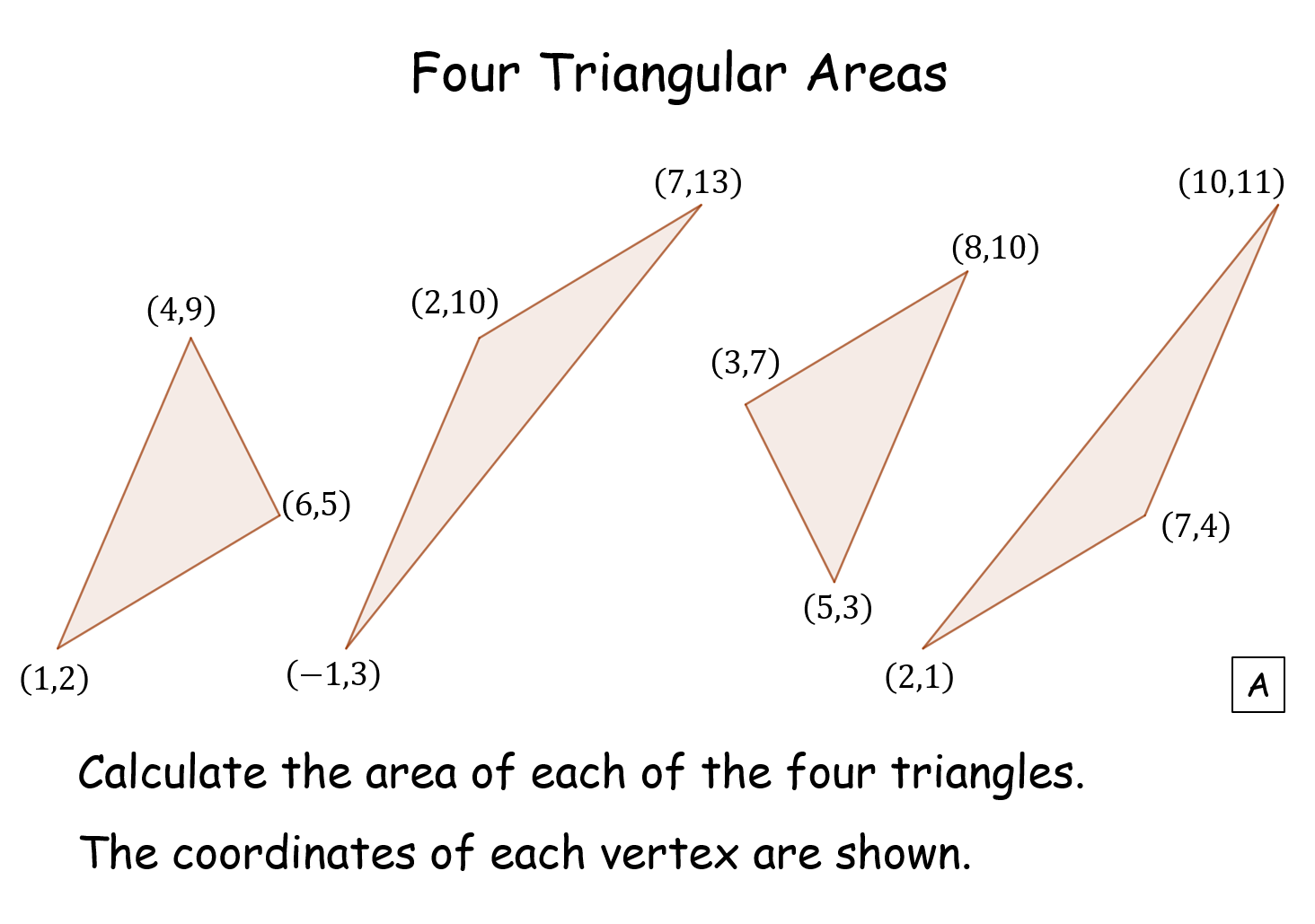
Four Triangular Areas |
Pupils are given the coordinates of the vertices of four triangles and they have to calculate their areas. They are all the same. But why, what links them? They bisect the same parallelogram and so all have the same area. Translations are involved in the analysis. An exploration of triangular areas activity is suggested.Four Triangular Areas |
C_
Year 9
x_C_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 78 |
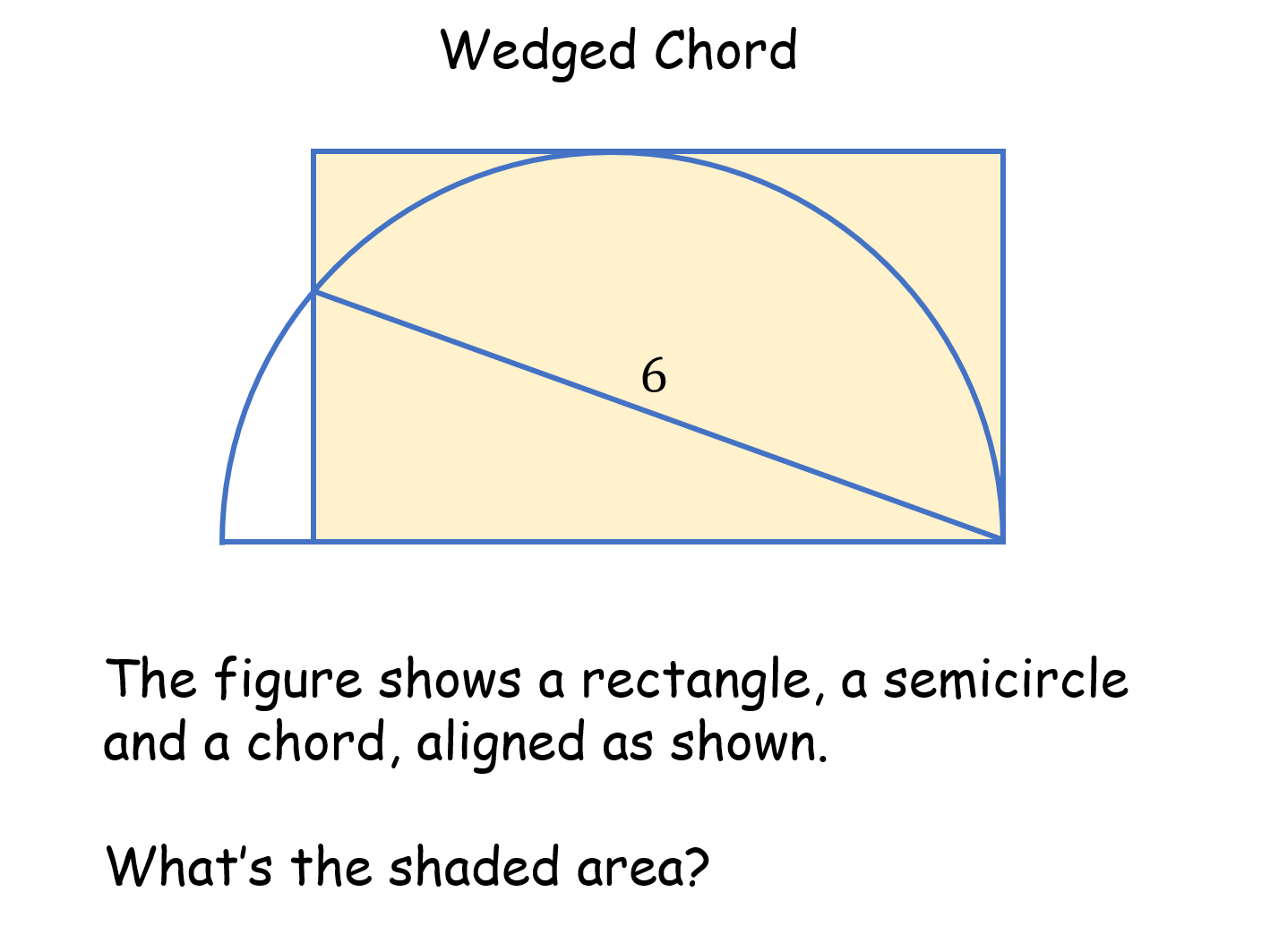
Wedged Chord |
This is a minimal information problem: there is only one number given! At first sight pupils will wonder if it is solvable at all. A great example of being stuck. The solution can be found using the intersecting chords theorem. 6th formers may use a circle theorem and a double angle formula. There is a twist at the end.Wedged Chord |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 79 |
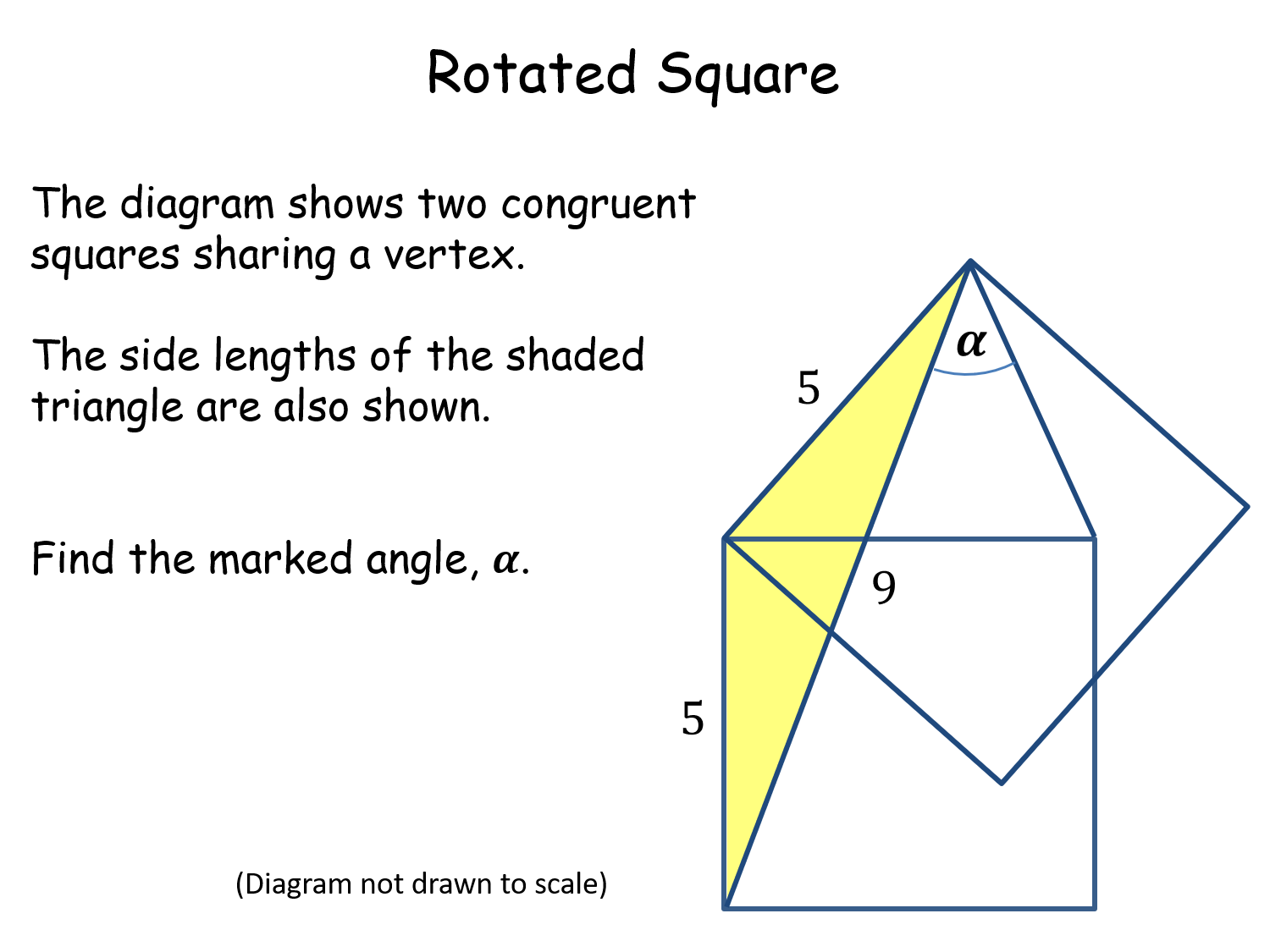
Rotated Square |
If the pupils have covered the Cosine Rule they may well set about calculating angles, which could be good revision. However, that is not necessary, and the given lengths are irrelevant! There is a nice solution using a circle theorem.Rotated Square |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 80 |
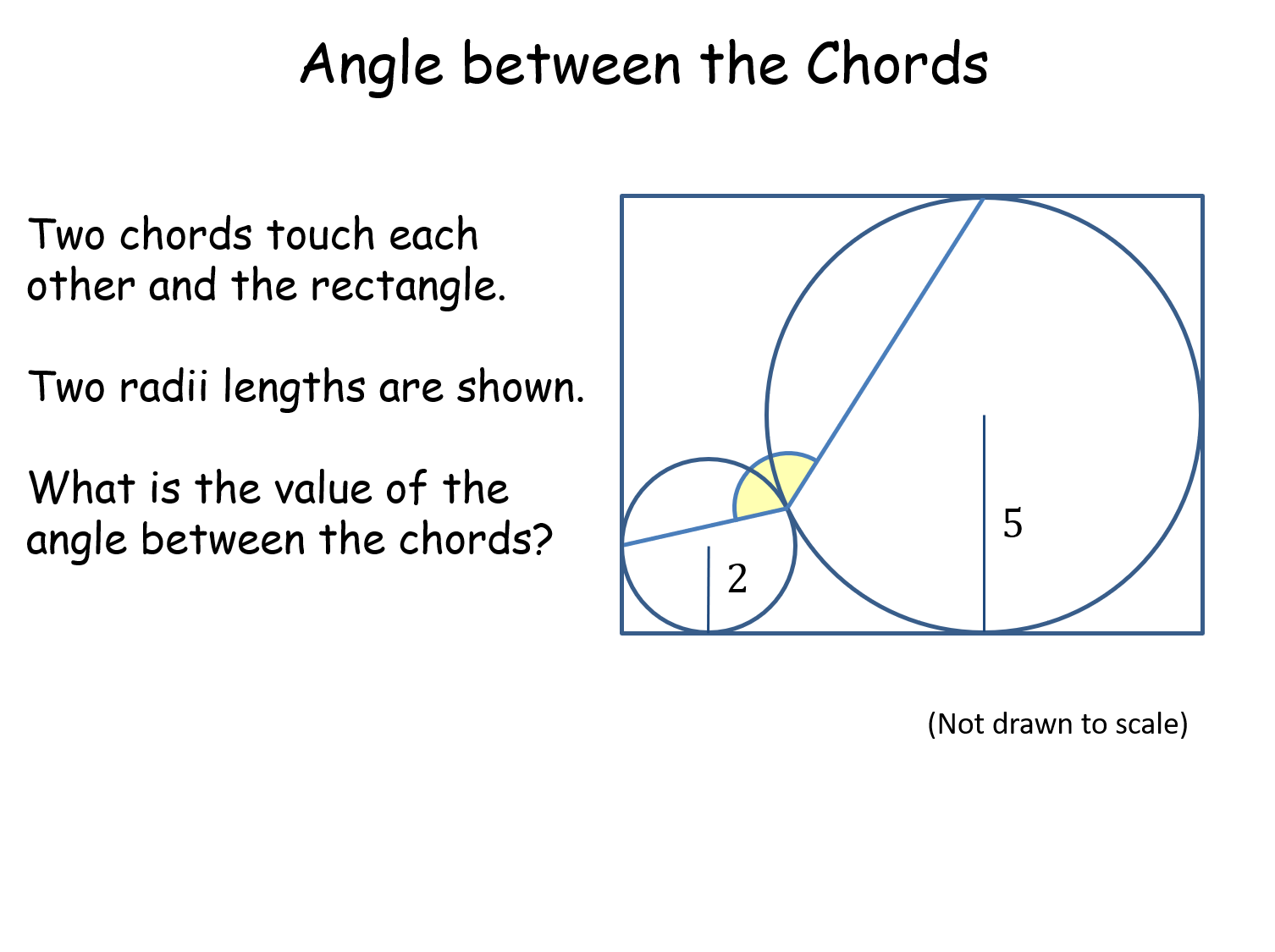
Angle between the Chords |
This is an example of misdirection. Triangles can be drawn and angles calculated to arrive at the answer (and did they use their calculator correctly and get an exact, not "rounds to", answer?). But none of that is necessary. By planning your way through this problem you find that the answer is invariant, with a few ways to solve it.Angle between the Chords |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 81 |
Three Equilateral Triangles |
Nothing too advanced here except the need to problem solve. Simple trigonometry is involved as well as spotting the need to use Pythagoras' Theorem. The result is unexpected and makes it easy for Teacher to know if they got it right. There is an animation in Geogebra to convince pupils of the result.Three Equilateral Triangles |
F
Year 1 - Pure
x_R_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 82 |
Tim and Tan |
Not too difficult a puzzle to solve but the wow factor is that all of their answers are the same. This is quite powerful at this age. So the question to the class is "How are all the answers the same?". This introduces some algebra to prove the general case.Tim and Tan |
A_
Year 7
x_A_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 83 |
Three Squares and a Semicircle |
This is one of those nice problems where most pupils will think that here isn't enough information to go on. Two solutions (using the intersecting chords theorem and Pythagoras) are shown. The numbers have been chosen to give some practice using surds and it is very easy for the teacher to know the answer to each worksheet.Three Squares and a Semicircle |
D_
Year 10
x_D_x |

|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
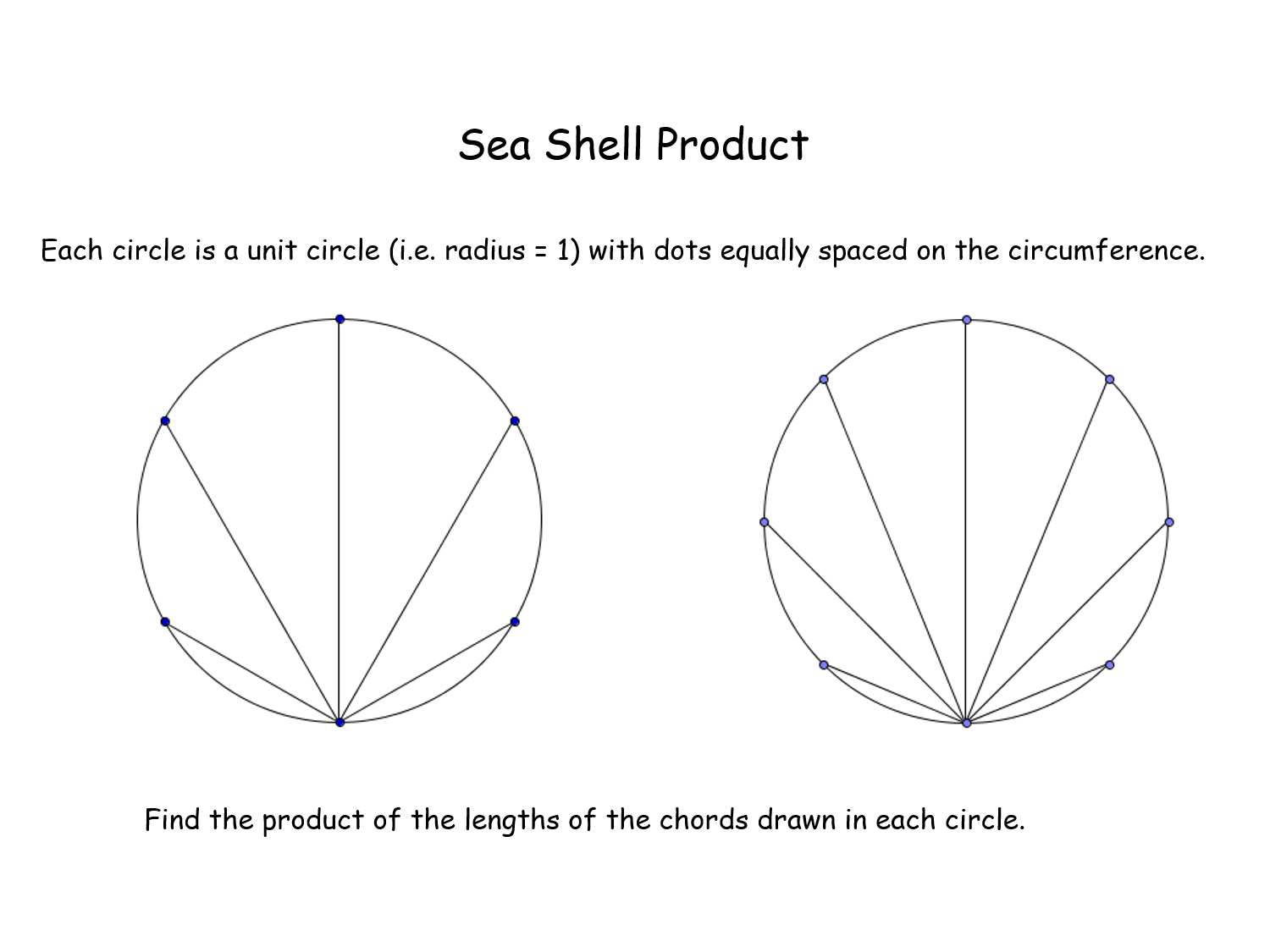
| 84 |
Sea Shell Product |
Pupils discover an intriguing result - the product of the lengths of the chords equals the number of equally spaced dots on the circle. Quite simple trigonometry and lengths of sides of triangles involving surds. The proof is very difficult, involving the nth roots of 1, and is well worth seeing.Sea Shell Product |
M
Year 2 - Further Pure
x_T_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 85 |
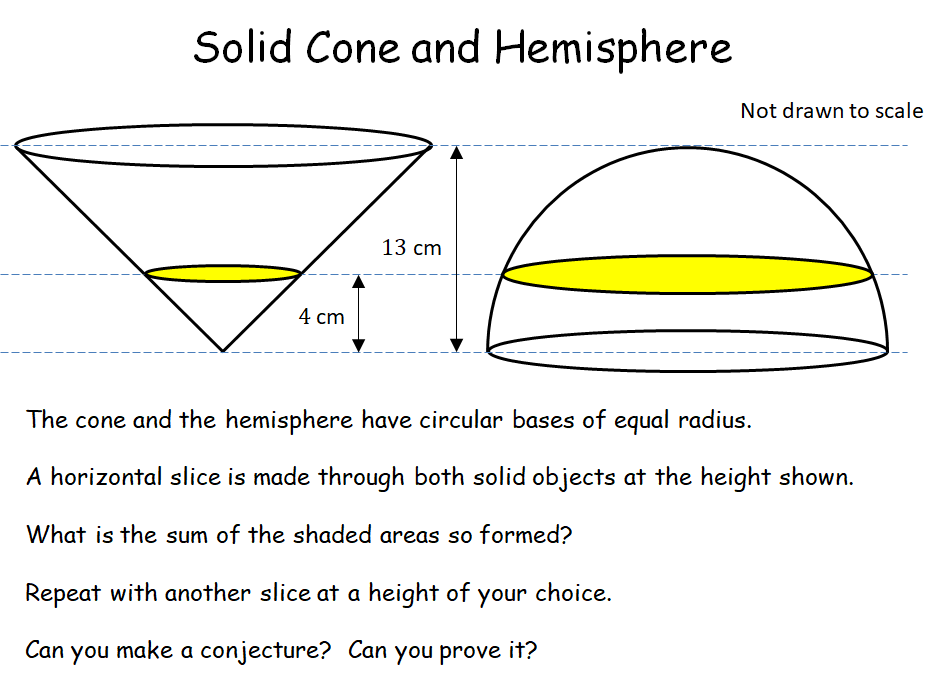
Solid Cone and Hemisphere |
A bit of history of Mathematics - working out the volume of sphere without calculus. Pupils have to work out the cross-sectional area of slices through a cone and a hemisphere, which some pupils find difficult to do. Remarkably, the sum of the areas is constant and equal to the base area of each solid. This leads into the idea of summing all of the areas to make up a volume.Solid Cone and Hemisphere |
E_
Year 11
x_E_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 86 |
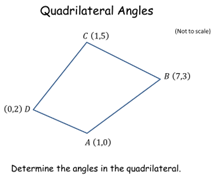
Quadrilateral Angles |
This problem tests pupils' understanding of coordinate geometry, i.e. the gradient of a line, the distance between two points, perpendicular lines, the equation of a line through two points. It assumes that they have not covered the Cosine Rule. This is addressed in task no. 87. All the answers are the sameQuadrilateral Angles |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 87 |
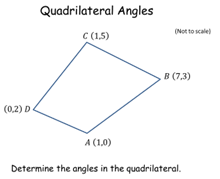
Quadrilateral Angles |
This problem is identical to task no. 86 but assumes that the pupils will use the Cosine Rule to solve it.Quadrilateral Angles |
F
Year 1 - Pure
x_R_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 88 |
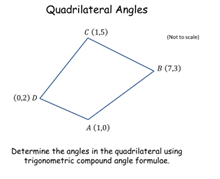
Quadrilateral Angles |
This problem is identical to task no. 86 but the pupils are encouraged to use trigonometric compound angle formulae to solve it. They are then shown how the quadrilaterals were produced and encouraged to prove the result with a little algebra.Quadrilateral Angles |
J
Year 2 - Pure
x_T_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|
| 89 |
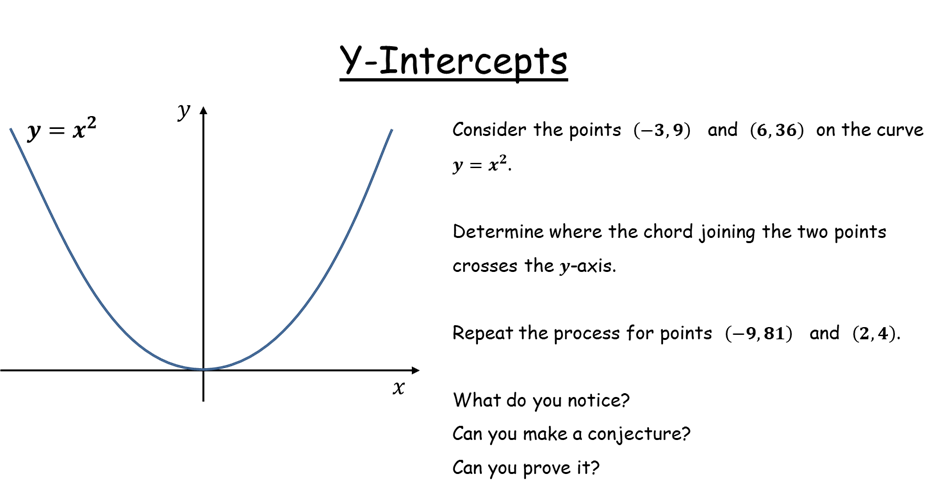
Y-Intercepts |
This problem tests pupils' ability to determine the equation of a straight line from the coordinates of two points on it and hence the y-intercept. But there is a surprise since another pair of coordinates delivers the same result! Can they work out why? More practice on proof. Answers are not all the same but easy to work out by the teacher.Y-Intercepts |
C_
Year 9
x_C_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 90 |
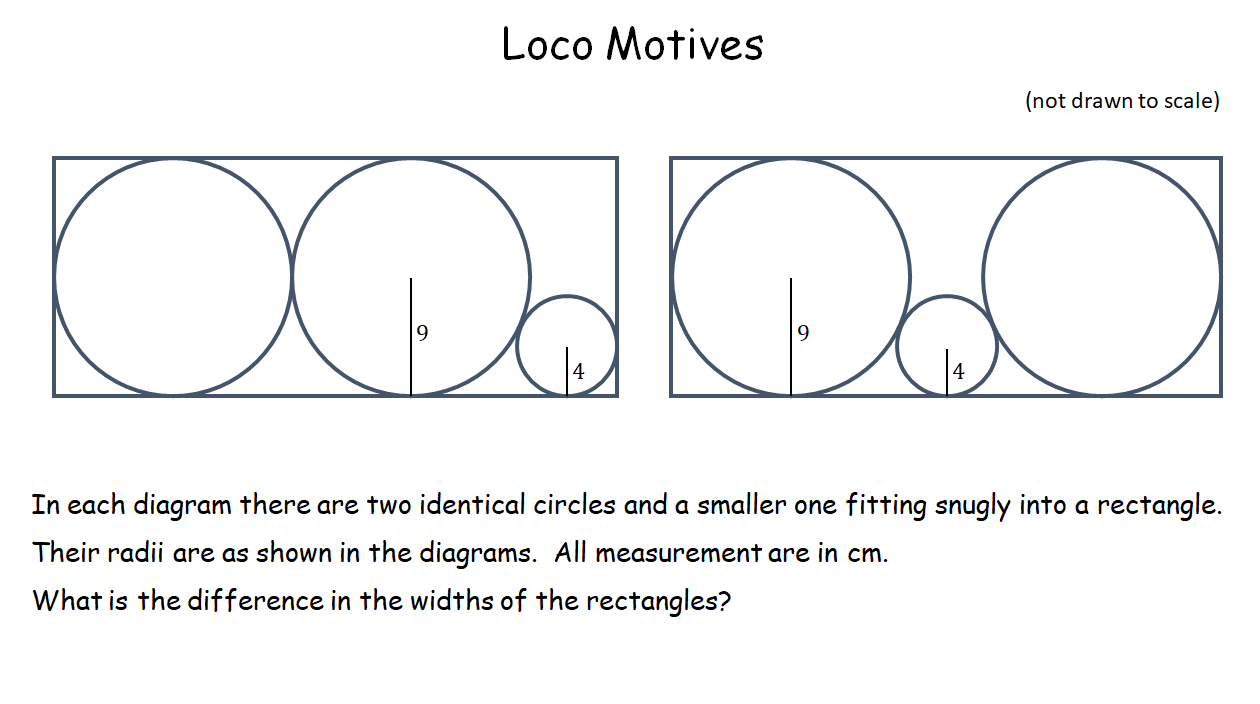
Loco Motives |
Three circles are packed into two rectangles in different ways and the difference between the rectangle widths is required. Not difficult, since it only requires use of Pythagoras' Theorem. But why are all the answers the same? A small amount of investigation is required and then pupils are required to prove their conjecture.Loco Motives |
D_
Year 10
x_D_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 91 |
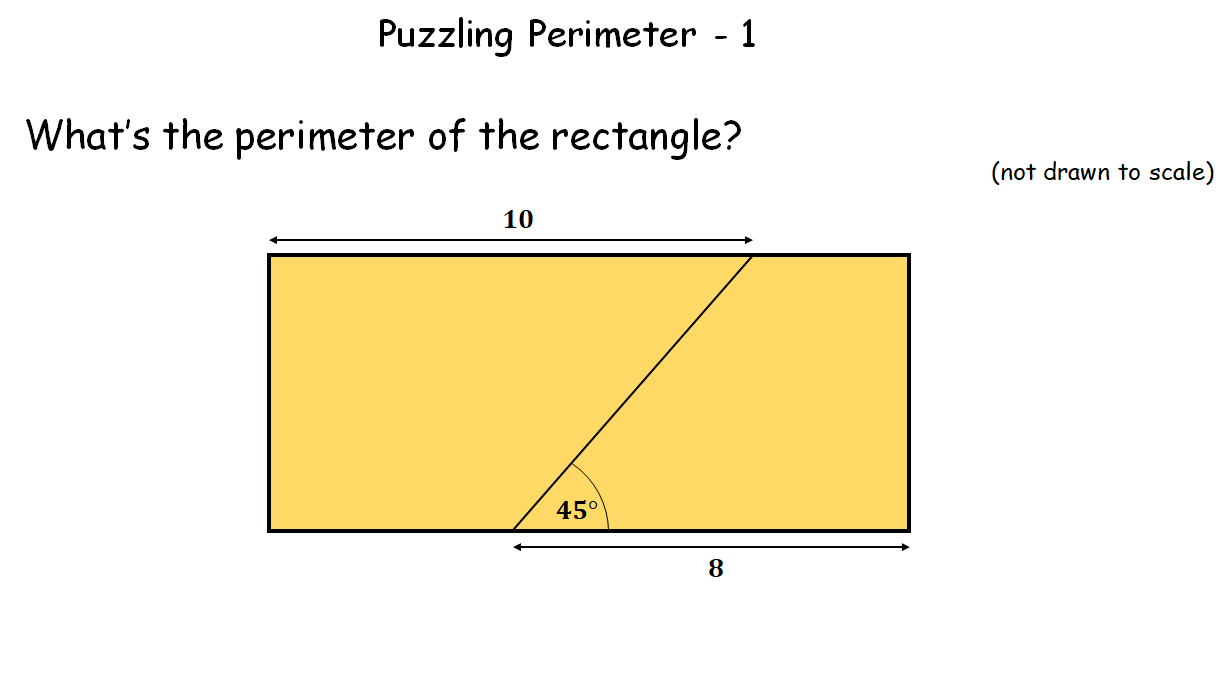
Puzzling Perimeter - 1 |
At first glance it looks like there isn't enough information to solve this puzzle, but it is quite striaghtforward, really. By defining a couple of variables, an expression for the perimeter can be determined and the variables later cancel out, showing that an infinite number of rectangles have the same perimeter!Puzzling Perimeter - 1 |
C_
Year 9
x_C_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 92 |
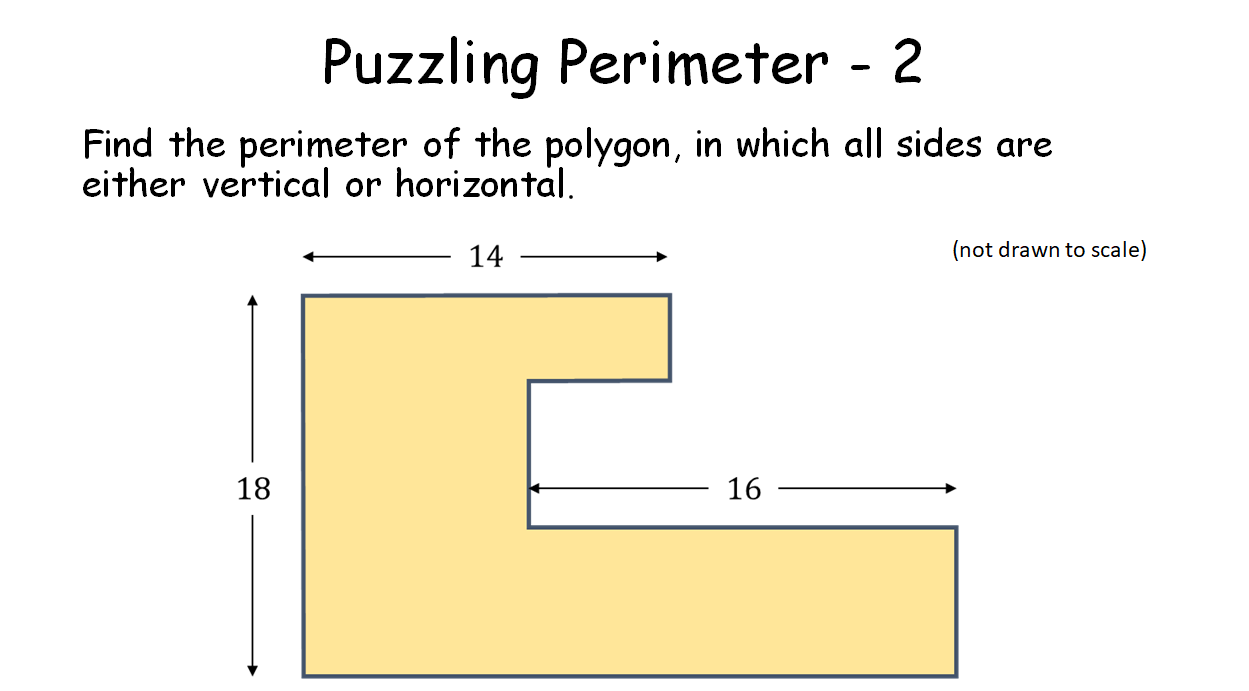
Puzzling Perimeter - 2 |
This is similar to "Puzzling Perimeter - 1" in the sense that it requires variables to be specified and equations built and then solved. All of the answers are the same. But there is a very neat solution involving translation of part of the perimeter, which would be good for the pupils to see.Puzzling Perimeter - 2 |
C_
Year 9
x_C_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 93 |
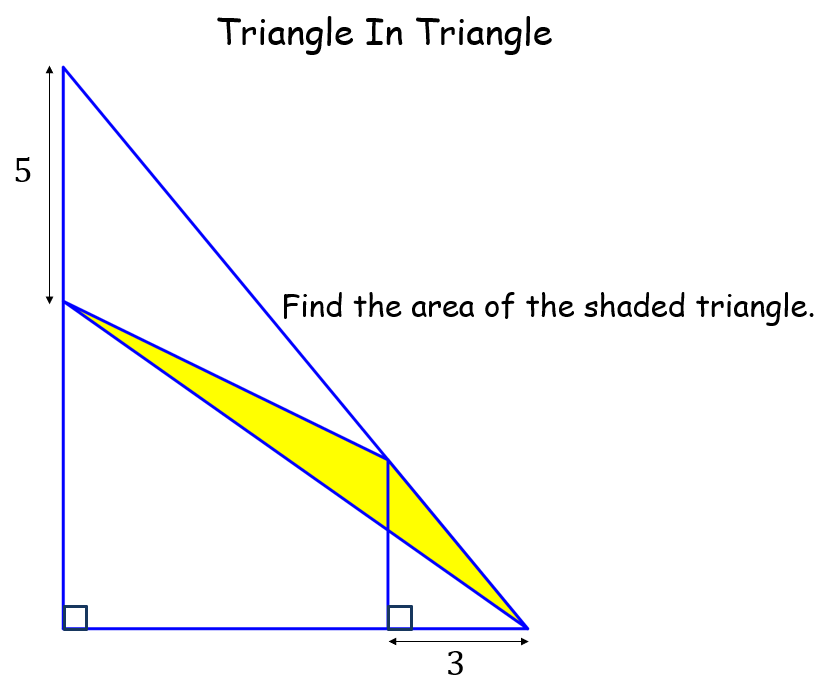
Triangle in Triangle |
At first glance it looks like there isn't enough information to solve this puzzle, but it is quite straight forward, really. By defining a couple of variables, expressions for areas of triangles can be determined. Using area subtraction an expression can be formed whereby the introduced variables cancel out.Triangle in Triangle |
B_
Year 8
x_B_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 94 |
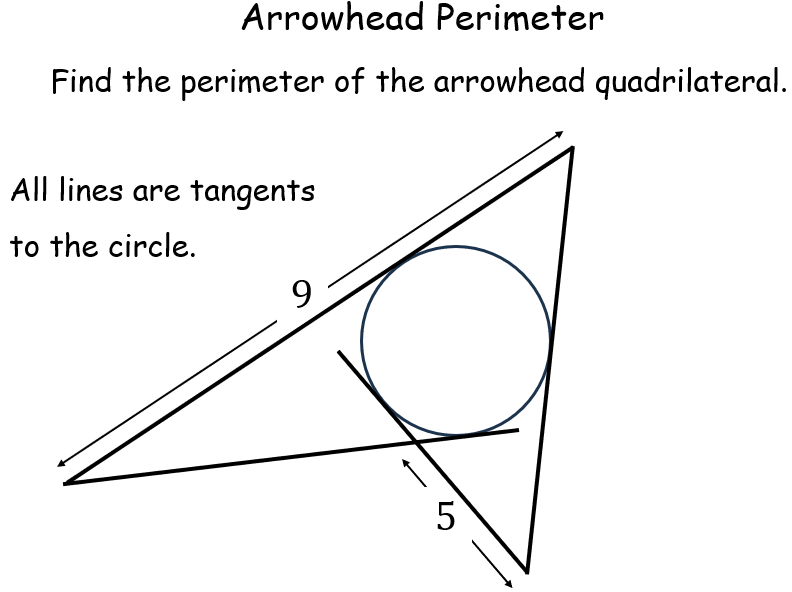
Arrowhead Perimeter |
Another problem that looks difficult but, in fact, isn't. It uses the fact that external tangents from a given point to a circle are equal in length. Can the pupils work that out themselves? Then it's just a case of creating some variables for unknown lengths, then forming a simple expression for the perimeter which simplifies to the answer.Arrowhead Perimeter |
C_
Year 9
x_C_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
 (Geogebra) (Geogebra) |
|
|
| 95 |
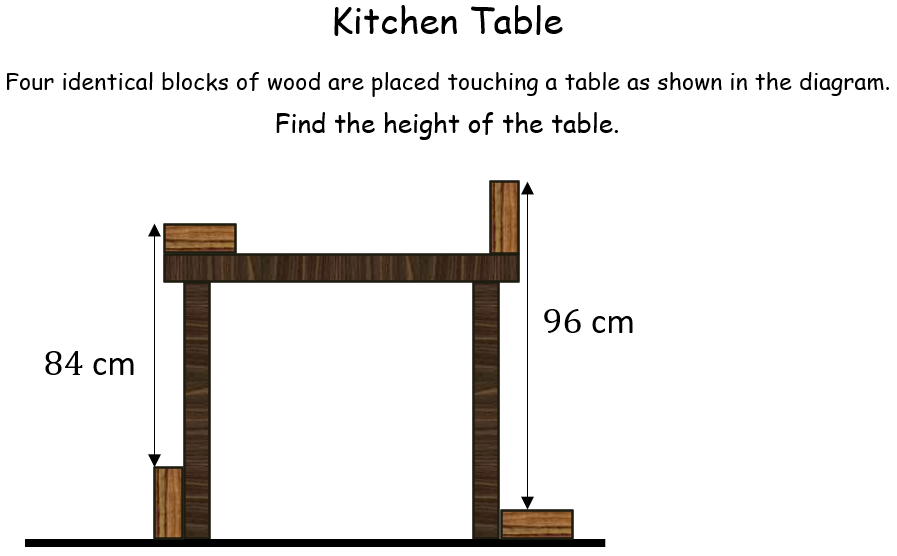
Kitchen Table |
A fairly simple problem taken from a UKMT Junior Mathematics Challenge paper. It requires letters to be assigned to unknown lengths and then simple algebra to solve a pair of simultaneous equations.Kitchen Table |
B_
Year 8
x_B_x |
|  (Adobe PDF) (Adobe PDF) |
 (PowerPoint) (PowerPoint) |
|
|
|